Bonjour,
Voici un autre exercice de Topologie pour lequel j'aurais besoin de votre aide :
1) Soit

un espace métrique. Montrer que
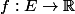
est continue ssi pour tout
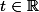
les ensembles
\leq t\})
et
\geq t\})
sont fermés.
2) Soient

un espace métrique,

un espace métrique compact et
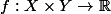
une fonction continue. On pose
=\sup_{y\in Y}f(x,y))
et
=\inf_{y\in Y}f(x,y).)
Montrer que

et

sont des fonctions continues sur
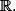
Pour
(1), je dis que si
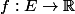
est continue, alors pour tout fermé

de

,
)
est un fermé de
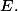
En particulier,
)
et
)
sont fermés.
Mais pour la réciproque, j'ai besoin de votre aide ! En effet, j'ai trouvé la piste suivante, qui ne me satisfait pas complètement :
Si pour tout
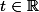
les ensembles
\leq t\})
et
\geq t\})
sont fermés, alors pour tout
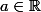
et pour tout
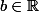
les ensembles
>a\})
et
0.)
La question est «existe-t-il
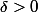
tel que pour tout
)
,
-f(x)|<\varepsilon)
» ?
Cela équivaut à se demander : «est-ce-que
-\varepsilon,f(x)+\varepsilon[))
est un voisinage de

» ?
Et la réponse est oui car c'est un
ouvert contenant
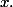
Peut-être auriez-vous une autre piste, plus rapide ?
Mais pour le (2), je ne vois pas du tout comment faire !Bien sûr, on peut commencer par fixer un
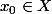
afin de montrer que

est continue en
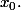
Puis j'utilise la compacité de

pour dire que le sup de la fonction continue
)
est atteint. Donc
 = f(x_0,y_0))
, le

dépendant (uniquement) de
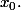
J'aboutis donc à
=f(x,y_x).)
Mais le problème est qu'on ne sait rien à priori de la continuité de
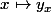
, n'est-ce pas ?
Merci d'avance pour vos suggestions !
Cordialement,
Niels.
