Défi 2.11
Olympiades mathématiques, énigmes et défis
yos
Membre Transcendant Messages: 4858Enregistré le: 10 Nov 2005, 20:20
yos » 13 Juin 2007, 17:46
Soit
une suite à termes positifs telle que la série
converge.
Montrer que la série
converge.
Foussa
Membre Naturel Messages: 15Enregistré le: 12 Juin 2007, 07:30
Foussa » 13 Juin 2007, 18:03
Du haut de mes 11 ans ... je ne sais c'est pas faire ça ! :hum:
yos
Membre Transcendant Messages: 4858Enregistré le: 10 Nov 2005, 20:20
yos » 13 Juin 2007, 18:08
C'est vrai que les anciens défis étaient hébergés dans la rubrique supérieur. Mon énoncé est effectivement peu adapté à la rubrique énigme. J'essaierai de faire mieux la prochaine fois.
Imod
Habitué(e) Messages: 6482Enregistré le: 12 Sep 2006, 11:00
Imod » 13 Juin 2007, 18:09
Il n'y a pas de dessins animés ou un quelconque star-ac à la télé ?
Imod
Imod
Habitué(e) Messages: 6482Enregistré le: 12 Sep 2006, 11:00
Imod » 13 Juin 2007, 18:17
Oups :marteau:
J'ouvre un défi pour Foussa pour me faire pardonner : abordable dès le primaire :we:
Imod
fahr451
Membre Transcendant Messages: 5142Enregistré le: 05 Déc 2006, 23:50
fahr451 » 13 Juin 2007, 20:50
deux cas
yos
Membre Transcendant Messages: 4858Enregistré le: 10 Nov 2005, 20:20
yos » 13 Juin 2007, 22:08
Bien vu Fahr. J'ai mis 2 à la place de e sinon j'ai fait la même chose.
fahr451
Membre Transcendant Messages: 5142Enregistré le: 05 Déc 2006, 23:50
fahr451 » 13 Juin 2007, 22:17
comme disait un de mes professeurs pour l 'analyse faut mettre les mains dans le cambouis
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider
gratuitement sur
Maths-forum !
Créé un compte en 1 minute et pose ta
question dans le forum ;-)
Inscription gratuite
) une suite à termes positifs telle que la série
une suite à termes positifs telle que la série 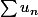 converge.
converge.^{1-\frac{1}{n}}) converge.
converge.