Probleme d'integrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 12 Juin 2007, 22:05
par reckahomis1 » 12 Juin 2007, 22:05
salu
f continue sur (a,b) et f(a+b-x)=f(x)
montrer que : a§b x*f(x) dx = a§b (a+b)/2 * f(x) dx
merci d'avance
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Juin 2007, 22:09
par yos » 12 Juin 2007, 22:09
'soir.
chgt de var u=a+b-x
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 12:00
par reckahomis1 » 13 Juin 2007, 12:00
yos a écrit:'soir.
chgt de var u=a+b-x
ca ne me donne rien, car ca va etr la meme expression f(u)=f(a+b-u)
tu px me dire ta methode pas à pas ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Juin 2007, 12:14
par mehdi-128 » 13 Juin 2007, 12:14
Bonjour,avec ce changement de variable,j'obtiens:
I=in([a...b]) (a+b-u).f(u).du .....
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 13:28
par reckahomis1 » 13 Juin 2007, 13:28
mehdi-128 a écrit:Bonjour,avec ce changement de variable,j'obtiens:
I=in([a...b]) (a+b-u).f(u).du .....
donc ca ne ddonne rien
on tombe sur la meme formule !!? :dodo:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Juin 2007, 13:32
par fahr451 » 13 Juin 2007, 13:32
en fait il suffit de savoir
que si
C = D- C alors C = D/2
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 13:34
par reckahomis1 » 13 Juin 2007, 13:34
si on pose u=a+b-x
dx=-du
donc a§b x*f(x) dx = a§b (a+b-u) f(a+b-u) du
comment on px trouvé a§b (a+b)/2 * f(x) dx ????
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 13:38
par reckahomis1 » 13 Juin 2007, 13:38
fahr451 a écrit:en fait il suffit de savoir
que si
C = D- C alors C = D/2
loooool
donc tu di ke f(a+b-x)=f(x) a+b-x=x alors x=(a+b)/2
mais c faux
stp regarde, a+b-x et x ont la meme image pas le contrair
fai un ptit chéma
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 13 Juin 2007, 13:38
par kazeriahm » 13 Juin 2007, 13:38
tu prend l'égalité que tu as écrit, tu remplace en sachant que f(a+b-u)=f(u),
tu as donc int(x*f(x) dx,a,b)=int((a+b)*f(x) dx,a,b)-int(x*f(x) dx,a,b) donc...
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 13:50
par reckahomis1 » 13 Juin 2007, 13:50
kazeriahm a écrit:tu prend l'égalité que tu as écrit, tu remplace en sachant que f(a+b-u)=f(u),
tu as donc int(x*f(x) dx,a,b)=int((a+b)*f(x) dx,a,b)-int(x*f(x) dx,a,b) donc...
j'ai pa bien compri mon ami
tu px bien expliqué ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 13 Juin 2007, 13:54
par kazeriahm » 13 Juin 2007, 13:54
euhhhhh, c'est difficile d'etre plus explicite, écris tout ca sur un papier, regarde ce que tas dit fahr, ce que je tai dit et normalement tu y arriveras
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 13 Juin 2007, 13:58
par reckahomis1 » 13 Juin 2007, 13:58
kazeriahm a écrit:euhhhhh, c'est difficile d'etre plus explicite, écris tout ca sur un papier, regarde ce que tas dit fahr, ce que je tai dit et normalement tu y arriveras
bawé, je travaille sur un papier

mais a+b-x et x ont la meme image ca vau dire pa k'ils sont egaux
il a démaré par a+b-x=x, je pens ke c totalement faux
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 13 Juin 2007, 14:23
par kazeriahm » 13 Juin 2007, 14:23
fahr n'a pas dit ca...
il a fait ca pour C=int(x*f(x) dx,a,b) et D=int((a+b)*f(x)dx,a,b)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Juin 2007, 14:25
par Joker62 » 13 Juin 2007, 14:25
Au final tu te retrouveras avec une relation du genre :
I = int(a,b) (a+b)f(u)du - I
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Juin 2007, 14:54
par fahr451 » 13 Juin 2007, 14:54
reckahomis1 a écrit:loooool
donc tu di ke f(a+b-x)=f(x) a+b-x=x alors x=(a+b)/2
mais c faux
stp regarde, a+b-x et x ont la meme image pas le contrair
fai un ptit chéma
s'il te plait fais un petit effort intellectuel
on y gagnera tous
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Juin 2007, 15:31
par Joker62 » 13 Juin 2007, 15:31
J'crois que c'est toi qui fait un blocage là...
Le changement de variable conduit bien au résultat.
Fait un effort comme dit fahr.
-
reckahomis1
- Membre Naturel
- Messages: 23
- Enregistré le: 11 Juin 2007, 21:19
-
 par reckahomis1 » 14 Juin 2007, 10:09
par reckahomis1 » 14 Juin 2007, 10:09
Joker62 a écrit:J'crois que c'est toi qui fait un blocage là...
Le changement de variable conduit bien au résultat.
Fait un effort comme dit fahr.
bnj
pourquoi tu m'écris pas la mathode pas à pas ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 14 Juin 2007, 14:52
par kazeriahm » 14 Juin 2007, 14:52
je crois que tous ceux qui t'ont répondu ont décrit la méthode...
honnetement c difficile de faire une nouvelle réponse sans reprendre ce qui a déja été dit
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 14 Juin 2007, 15:21
par Pythales » 14 Juin 2007, 15:21
)
prend des valeurs symétriques par rapport au milieu du segment

. Du fait de cette symétrie,
f(x)dx)
soit
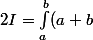f(x)dx)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
