Lever une FI
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 12 Juin 2007, 23:56
par Totally » 12 Juin 2007, 23:56
Bonsoir a tous, voila je n'arrive pas a lever cette fonction
;)(x²+x)-x
Donc ce que j'ai fait c'est mettre en facteur x ce qui donne x(;)(1+(1/x))-1)
Voila après je ne sais plus quoi faire. Merci de bien vouloir m'aider.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 13 Juin 2007, 00:00
par nekros » 13 Juin 2007, 00:00
Salut :)
Il faudrait peut-être nous dire en quoi tu cherches la limite :lol:
Sinon, un bon moyen est d'utiliser la quantité conjuguée :)
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 13 Juin 2007, 09:17
par Totally » 13 Juin 2007, 09:17
ah oui dsl en + infini.
Oui je sais pour la quantité conjugué mais est ce que ici je peux determiner la limite avec ca?
En faite ce qui me pose probleme c'est que je sais pas si lim de ;)(1+(1/x)) tend vers 1 ou 0 en + infini et donc ce qui ferait que la fonction tend vers - infini non ?
-
thomasg
- Membre Relatif
- Messages: 443
- Enregistré le: 06 Mai 2005, 09:45
-
 par thomasg » 13 Juin 2007, 09:26
par thomasg » 13 Juin 2007, 09:26
Bonjour,
Oui, en utilisant le conjugué:
V(x²+x)-x=x/(x(V(1+1/x)+1)=1/(V(1+1/x)-1), le dénominateur tend vers 0+ en +inf, donc la fonction tend vers +inf en +inf.
Remarque: ta proposition -inf ne peut pas être valable car le premier terme de la différence est toujours supérieur au second dans l'expression de ta fonction.
A bientôt.
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 13 Juin 2007, 09:39
par Totally » 13 Juin 2007, 09:39
D'accord j'ai compris merci.
J'aimerais savoir quelque chose en plus si ma fonction fait ca: x(;)(1+(1/x))-1)
Sans la conjugué ni rien est ce possible de determiner sa limite?
Sachant qu'on a trouvé que ;)(1+(1/x))-1 tend vers 0 en +00 donc x s'annule puisque son facteur tend vers 0 ou x tend vers +00 est la c'est encore une FI?
-
thomasg
- Membre Relatif
- Messages: 443
- Enregistré le: 06 Mai 2005, 09:45
-
 par thomasg » 13 Juin 2007, 09:48
par thomasg » 13 Juin 2007, 09:48
C'est ta dernière proposition la bonne, tu as encore une FI : +inf*0.
Intuitivement: En +inf V(x²+x) est infiniment plus grand que V(x²), mais tu ne peux pas rédiger comme cela,
pour une autre méthode, rien ne me vient à l'idée pour l'instant.
A bientôt.
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 13 Juin 2007, 09:50
par Totally » 13 Juin 2007, 09:50
Ok merci beaucoup. C'etait juste pour savoir s'il fallait vraiment conjugué ou pas.
C'est bon j'ai compris.
Merci.
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 13 Juin 2007, 10:13
par Totally » 13 Juin 2007, 10:13
Encore une derniere fonction deja conjugué (3+(2/x))/;)(4+(5/x²))+;)(1+(3/x²))
Je touve que ;)(4+(5/x²))+;)(1+(3/x²) tend vers 0 en +00 donc au denominateur il tend vers +00 docn la fonction tend vers +00 c'est ca ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Juin 2007, 10:25
par fonfon » 13 Juin 2007, 10:25
salut thomasg etant deconnecté...
c'est bien

si c'est ça ça tend vers 3 et non 0
et donc
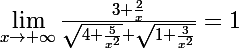
-
Totally
- Membre Naturel
- Messages: 11
- Enregistré le: 24 Avr 2007, 20:30
-
 par Totally » 13 Juin 2007, 10:38
par Totally » 13 Juin 2007, 10:38
D'accord c'est cool j'ai compris merci!!
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 13 Juin 2007, 10:39
par rene38 » 13 Juin 2007, 10:39
Bonjour
thomasg a écrit:Bonjour,
Oui, en utilisant le conjugué:
V(x²+x)-x=x/(x(V(1+1/x)+1)=1/(V(1+1/x)-1), le dénominateur tend vers 0+ en +inf, donc la fonction tend vers +inf en +inf.

-
thomasg
- Membre Relatif
- Messages: 443
- Enregistré le: 06 Mai 2005, 09:45
-
 par thomasg » 13 Juin 2007, 14:11
par thomasg » 13 Juin 2007, 14:11
Désolé ...
j'en profite pour signaler que mon pseudo-raisonnement par intuition est complètement faux.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 13 Juin 2007, 16:01
par rene38 » 13 Juin 2007, 16:01
j'en profite pour signaler que mon pseudo-raisonnement par intuition est complètement faux.
Ben oui puisque tu écrivais
En +inf V(x²+x) est infiniment plus grand que V(x²),
Or la différence est loin d'être infinie : elle tend vers 1/2.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités

