Primitive
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 11 Juin 2007, 16:10
par nekros » 11 Juin 2007, 16:10
Salut

Déterminer une primitive de :
ln(xln(x))ln(xln(xln(x)))+ln(x)+1}{ ln(x)ln(xln(x))}})
Bon courage
(avec la méthode, pour éviter d'utiliser Maple :ptdr: )
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 11 Juin 2007, 18:18
par nekros » 11 Juin 2007, 18:18
Pas d'idée ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Juin 2007, 18:49
par Nightmare » 11 Juin 2007, 18:49
Salut Nekros :happy3:
Si, plein d'idées, mais les calculs laborieux découragent souvent lol.
J'avais l'idée de poser u=ln(x)ln(xln(x)) et de reconnaitre du sans exprimer la réciproque mais j'ai des x au dénominateur en trop...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Juin 2007, 21:09
par fahr451 » 11 Juin 2007, 21:09
sisi ça donne envie
maple donne le résultat ?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 11 Juin 2007, 22:18
par nekros » 11 Juin 2007, 22:18
oui fahr :)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Juin 2007, 22:24
par Clembou » 11 Juin 2007, 22:24
fahr451 a écrit:sisi ça donne envie
maple donne le résultat ?
sur xcas, ça donne un résultat indescriptible... (dans le sens incroyable)

pour ceux qui veulent la calculer, bon courage

:)
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 11 Juin 2007, 22:38
par nekros » 11 Juin 2007, 22:38
Salut :)
Change de logiciel dans ce cas :lol:
Sur maple, cette primitive s'exprime en fonction que de deux ou trois log
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Juin 2007, 22:42
par Imod » 11 Juin 2007, 22:42
fahr451 a écrit:ça donne envie maple donne le résultat ?
nekros a écrit:oui fahr

Un exercice dont la solution est donnée par un logiciel perd 90% de son intérêt , mais bon , je n'aime pas l'analyse ( ce qui ne m'a pas empêcher d'avoir 16/20 à l'oral de l'agreg il y a fort longtemps ) .
Imod
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Juin 2007, 22:45
par Clembou » 11 Juin 2007, 22:45
nekros a écrit:Salut

Change de logiciel dans ce cas

Sur maple, cette primitive s'exprime en fonction que de deux ou trois log
A ok... parce que moi j'ai ça avec mon logiciel
+x\ln(\ln(x\ln(x))+)
[CENTER]
)^2\ln(x)^2-\ln(\ln(x))^2\ln(x)-2\ln(\ln(x))\ln(x)^3-2\ln(\ln(x))\ln(x)^2-\ln(x)^4-\ln(x)^3}{\ln(x\ln(x))\ln(\ln(x))^2\ln(x)^2+2\ln(x\ln(x))\ln(ln(x))\ln(x)^3+ln(x\ln(x))\ln(x)^4}+ \frac{\ln(x)^2+\ln(x)}{\ln(\ln(x))\ln(x)^2+\ln(x)^3} dx)
[/CENTER]
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Juin 2007, 22:46
par Nightmare » 11 Juin 2007, 22:46
Je propose le changement de variable :
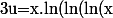)+ln(x))+xln(x)-x)
:lol2:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 12 Juin 2007, 13:26
par fahr451 » 12 Juin 2007, 13:26
Clembou a écrit:A ok... parce que moi j'ai ça avec mon logiciel
+x\ln(\ln(x\ln(x))+)
[CENTER]
)^2\ln(x)^2-\ln(\ln(x))^2\ln(x)-2\ln(\ln(x))\ln(x)^3-2\ln(\ln(x))\ln(x)^2-\ln(x)^4-\ln(x)^3}{\ln(x\ln(x))\ln(\ln(x))^2\ln(x)^2+2\ln(x\ln(x))\ln(ln(x))\ln(x)^3+ln(x\ln(x))\ln(x)^4}+ \frac{\ln(x)^2+\ln(x)}{\ln(\ln(x))\ln(x)^2+\ln(x)^3} dx)
[/CENTER]
là ça donne encore un peu plus envie
encore une tite transformation ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 12 Juin 2007, 13:29
par Clembou » 12 Juin 2007, 13:29
fahr451 a écrit:là ça donne encore un peu plus envie
encore une tite transformation ?
Lol

Essaie de calculer l'intégrale que donne mon log

:) Tu verras, elle est très sympa :zen:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 15 Juin 2007, 23:30
par Imod » 15 Juin 2007, 23:30
curiosité malsaine ,
ce problème a-t-il une solution ( humaine ) ?
Imod
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 12 Juil 2007, 09:48
par fibonacci » 12 Juil 2007, 09:48
bonjour;
int=x(ln(x*ln(x*ln(x)))-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités