Symetrie par rapport à la droite y=1/2 ??
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
alterganon
- Messages: 3
- Enregistré le: 04 Juin 2007, 08:48
-
 par alterganon » 04 Juin 2007, 08:56
par alterganon » 04 Juin 2007, 08:56
Bonjour tout le monde !
Je suis en train de faire le sujet de Pondichery 2002, et je bloque sur une question que je n'avais encore jamais vu en TS (et pourtant je commence à bien le connaitre ce programme !)
a) Montrer que pour tout réel x , les points M(x ; f0(x)) et M '(x ; f1(x)) sont symétriques par rapport à la droite d d'équation y = 1/2 .
avec

Est-ce encore dans le programme de TS ? Cela me semble bizzard, on nous apprend a trouver des symetrie par rapport à une droite x=k ou par rapport à un point, mais jamais par rapport à une droite...
Merci de votre aide !!
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 04 Juin 2007, 09:51
par nico74 » 04 Juin 2007, 09:51
=\frac{e^{x}}{1+e^{x}})
=\frac{e^{x}}{e^{x}(1+e^{x})}=\frac{1}{(1+e^{x})})
Cherches le point d intersection H de (MM') avec la droite (D) d'equation y=1/2.
Ensuite tu montres que
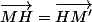
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 04 Juin 2007, 10:02
par nico74 » 04 Juin 2007, 10:02
C'est un peu tiré par les cheveux peut être.
Sinon on remarque que
=f_{1}(x-0,5))
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 04 Juin 2007, 10:12
par Quidam » 04 Juin 2007, 10:12
nico74 a écrit:C'est un peu tiré par les cheveux peut être.
Sinon on remarque que
=f_{1}(x-0,5))
C'est juste, mais cela ne démontre pas la symétrie demandée !
-
alterganon
- Messages: 3
- Enregistré le: 04 Juin 2007, 08:48
-
 par alterganon » 04 Juin 2007, 11:56
par alterganon » 04 Juin 2007, 11:56
je n'y suis toujours pas...
Mon point d'intersection est en x=0
Mais je ne vois pas comment démontrer le reste..
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 04 Juin 2007, 12:59
par emdro » 04 Juin 2007, 12:59
Tu auras une symétrie par rapport à d:y=1/2 si et seulement si pour tout x, f1(x)=1-f0(x); cela vient de [f0(x)+f1(x)]/2=1/2.
On utilise une telle symétrie moins souvent que par rapport à une droite verticale, car la courbe d'une fonction NE peut JAMAIS être symétrique par rapport à une droite horizontale . Ici, il s'agit de C0 et C1.
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 04 Juin 2007, 13:00
par nico74 » 04 Juin 2007, 13:00
Il faut chercher l'equation de la droite (MM')
Elle passe par les points
)
et
)
Son équation est donc
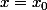
.
Le point d'intersection de (MM') et (D) est donc le point
)
Enfin
)=(0,\frac{1}{2}-\frac{e^{x_{0}}}{1+e^{x_{0}}})=(0,\frac{1+e^{x_{0}}-2e^{x_{0}}}{1+e^{x_{0}}})=(0,\frac{1-e^{x_{0}}}{1+e^{x_{0}}}))
et
-y_{H})=(0,\frac{1}{1+e^{x_{0}}}-\frac{1}{2})=(0,\frac{2-1-e^{x_{0}}}{1+e^{x_{0}}})=(0,\frac{1-e^{x_{0}}}{1+e^{x_{0}}}))
Et donc
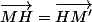
D'ou la symétrie
C'est une démonstration rigoureuse mais je pense qu il y a plus simple
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 04 Juin 2007, 13:06
par emdro » 04 Juin 2007, 13:06
Pour Nico 74,
c'est effectivement rigoureux, sauf l'égalité entre coordonnées. Cela ne se fait pas trop au lycée. Essaie d'éviter.
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 04 Juin 2007, 13:22
par nico74 » 04 Juin 2007, 13:22
Pourtant deux vecteurs sont égaux s ils ont même abscisse et même ordonnée.
Je pense que celà se voit au lycée
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 04 Juin 2007, 13:32
par emdro » 04 Juin 2007, 13:32
Bien d'accord, mais on manipule assez peu les coordonnées en temps que couple. On ne définit pas la somme de deux couples non plus. Donc on préfère éviter l'égalité entre deux couples.
Ecris u(1+2;3+8) donc u(3;11) plutôt que u(1+2;3+8)=(3;11).
Quel serait d'ailleurs le membre de gauche de cette dernière égalité? Le vecteur u, ses coordonnées? Tu vois qu'on arrive très vite à des approximations...
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 04 Juin 2007, 14:23
par nico74 » 04 Juin 2007, 14:23
Tu as raison emdro, il faut réecrire à chaque fois u(1+2,7-3) d'ou u(3,4) et sans le signe égal.
-
alterganon
- Messages: 3
- Enregistré le: 04 Juin 2007, 08:48
-
 par alterganon » 05 Juin 2007, 09:55
par alterganon » 05 Juin 2007, 09:55
Merci beaucoup, j'ai tout compris maintenant !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités

