[Dénombrement]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 03 Juin 2007, 15:16
par max » 03 Juin 2007, 15:16
Bonjour
Je dois déterminer le plus grand entier k tel que 1000! est divisible par 2^k
Comment puis je procéder ?
Merci beaucoup
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Juin 2007, 15:24
par aviateurpilot » 03 Juin 2007, 15:24
max a écrit:Bonjour
Je dois déterminer le plus grand entier k tel que 1000! est divisible par 2^k
Comment puis je procéder ?
Merci beaucoup
c'est facile, c'est just
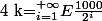)
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 03 Juin 2007, 15:25
par max » 03 Juin 2007, 15:25
aviateurpilot a écrit:c'est facile, c'est just
)
je n'ai pas vu de sommes "infinies"
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Juin 2007, 15:27
par aviateurpilot » 03 Juin 2007, 15:27
c'est une somme fini puisqu'il s'annul a partir d'un cetrain rang
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 03 Juin 2007, 15:28
par max » 03 Juin 2007, 15:28
aviateurpilot a écrit:c'est une somme fini puisqu'il s'annul a partir d'un cetrain rang
je suis en MPSI et je n'ai jamais entendu parler de sommes de ce genre
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Juin 2007, 15:34
par aviateurpilot » 03 Juin 2007, 15:34
max a écrit:je suis en MPSI et je n'ai jamais entendu parler de sommes de ce genre
moi aussi je suis en MPSI
je pense qu'on vu en MPSI
=\bigsum_{i=0}^{+\infty}a_ix^i)
avec (a_i) suit qui s'annul a partir d'un cetrain rang
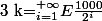=[1000/2]+[1000/4]+[1000/8]+...+[1000/2^9])
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 03 Juin 2007, 15:37
par max » 03 Juin 2007, 15:37
non on ne l'a pas vu.
on étudie la leçon sur le dénombrement, c'est donc surement ce qu'il faut utiliser ici, mais je ne trouve pas
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Juin 2007, 15:44
par aviateurpilot » 03 Juin 2007, 15:44
max a écrit:non on ne l'a pas vu.
on étudie la leçon sur le dénombrement, c'est donc surement ce qu'il faut utiliser ici, mais je ne trouve pas
oui, pur trouver k on a que calculer le nombre des multiple de 2 , de 4 de 8....jusqu'a

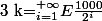=[1000/2]+[1000/4]+[1000/8]+...+[1000/2^9])
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 03 Juin 2007, 16:40
par alben » 03 Juin 2007, 16:40
Bonsoir,
Tu peux raisonner plus simplement en constatant :
-que les nombres pairs apportent chacun un facteur 2. Il y en a 500
-que les multiples de 4 ajoutent un deuxième facteur 2 (le premier a déjà été compté)-->+250 facteurs 2
-que les multiples de 8.....
etc jusquà 512
Ce qui te donnes exactement le résultat d'aviateurpilot !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
