Problème avec les matrices

par **nicco** » 30 Mai 2007, 21:40

Bonjour, j'aimerai que l'on m'aide pour cet exercice :

Les lettres i et j désignent des nombres entiers naturels compris entre 1 et 4.
Une firme fabrique quatre produits Pi, 1< i < 4. Au cours du processus de fabrication, les pièces produites peuvent entrer dans la fabrication d'éléments intermédiaires ou de produits finis.
Les données technologiques sont les suivantes : P1 est fabriqué directement à partir des matières premières; la fabrication d'une unité de P2 nécessite, en plus des matières premières, deux unités de P1; celle d'une unité de P3 nécessite une unité de P1 et une de P2; enfin une unité de P4 demande une unité de P1 et deux de P3.
On fait les hypothèses simplificatrices d'additivité et de rendements constants et on se propose de déterminer le programme (c'est à dire la production totale de chaque produit) nécessaire pour satisfaire une commande extérieure donnée.

1) Ecrire la matrice A=(a i j) dite des productions intermédiaires, dans laquelle, pour tout couple (i, j), le coefficient a i j représente le nombre d'unités du bien Pi nécessaire à la fabrication d'une unité du bien Pj.

2) Soit C=(c i) 1< i < 4 une matrice unicolonne représentant une commande extérieure donnée et X=(x i) 1< i < 4 une matrice unicolonne représentant un programme nécessaire à la satisfaction de C. Que représente le produit AX? Etablir que X=C+AX.

3) Déterminer le programme nécessaire à la réalisation d'une commande extérieure de cent unités de chaque produit.

Alors, j'explique un peu mon problème :
déjà pour la première question dont je ne suis pas certain de la réponse que j'ai trouvé (mais je doute vraiment que ce soit le bon résultat) :
0 0 0 0
2 0 0 0
1 1 0 0
1 0 2 0
Ensuite la deuxième, j'ai essayé plusieurs matrices mais en fin de compte je ne trouve pas le bon résultat puisque je n'arrive pas à établir que X=C+AX.
Enfin la troisième, j'ai tenté de multiplier par 100 la matrice de la question 1) mais je pense pas que ce soit la bonne méthode.

par **nicco** » 02 Juin 2007, 14:47

je remonte le sujet, vu que j'ai pas de réponse, si quelqu'un pouvait m'aider ça serait sympa, merci

par **jeanne** » 03 Juin 2007, 10:41

Bonjour!
Moi aussi j'ai un petit problème...
Quand je diagonalise une matrice 3x3 et que je trouve 2 valeurs propres a1 et a2 et que dimE1 = 2 et dimE2 = 1, comment s'écrit alors la matrice diagonale?
Est-ce :
a1 0 0
0 a1 0
0 0 a2

?

par **yos** » 03 Juin 2007, 10:50

jeanne a écrit:Bonjour!
Moi aussi j'ai un petit problème...
Quand je diagonalise une matrice 3x3 et que je trouve 2 valeurs propres a1 et a2 et que dimE1 = 2 et dimE2 = 1, comment s'écrit alors la matrice diagonale?
Est-ce :
a1 0 0
0 a1 0
0 0 a2

?

Oui c'est ça mais tu aurais dû ouvrir un autre fil car Nicco attend des réponses.

par **fahr451** » 03 Juin 2007, 10:51

bonjour jeanne

il te faut ouvrir un NOUVEAU post et ne pas "polluer" celui d'un autre

par **jeanne** » 03 Juin 2007, 10:54

ok désolée... ce n'était pas mon intention...

par **yos** » 03 Juin 2007, 11:00

Pour Nicco :
1) tu as inversé lignes et colonnes il me semble :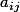

est le terme de la ligne i et de la colonne j.

2) Je pense que X est une liste de 4 nombres entiers désignant le nombre de pièces de chaque type à produire pour satisfaire la commande. Il faut en produire plus que celles de la commande car il faut prendre en compte les pièces qui servent à fabriquer les pièces. AX c'est la matrices (unicolonne) qui donne le nombre de pièces nécessaires pour le "programme". On lui ajoute les pièces de la commande et on a le contenu du programme.

3) Tu travailles avec C=(100\100\100\100) (en colonnes) et tu résous le système d'inconnue X=(x,y,z,t) (en colonnes)

Problème avec les matrices

problème avec les matrices

Qui est en ligne