Analyse complexe

par **Ptah Sokar** » 29 Mai 2007, 10:53

Bonjour à tous,

J'ai un petit problème, je ne vois pas clairement la démarche à suivre pour écrire un développement de Laurent ainsi que pour calculer le résidu... Si quelqu'un pouvait m'éclairer...

Par exemple, aux partiels, j'avais eu : f(z) = 1/(z^3 - 2z²) et il fallait écrire le développement de Laurent en 0 de f(z) dans l'anneau {z | |z| > 2} ainsi que calculer Res(f(z),0) et j'ai été incapable de le faire...

Merci a tous pour vos conseils !

:zen:

par **yos** » 29 Mai 2007, 12:33

Moi j'écrirais :

.
C'est le DSL(f,0).
Le résidu est le coef de

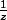
, c'est-à-dire -1/4.

par **yos** » 29 Mai 2007, 12:39

Et c'est pour 0<|z|<2 .
Un DSL est toujours défini dans une couronne et pas l'extérieur d'un disque comme tu l'as écrit.

par **iamsebfont** » 29 Mai 2007, 16:22

C'était peut-être la couronne de rayon R1 = 2 et R2 = +infini
Non ?

par **yos** » 29 Mai 2007, 16:24

Ben y faudrait que la partie n>0 du DSL soit de rayon de convergence infinie.

par **nekros** » 31 Mai 2007, 22:29

[quote="yos"]Et c'est pour 01[/TEX] ie à l'extérieur du disque.

Qu'en penses-tu ?

Merci

par **yos** » 01 Juin 2007, 11:34

Tu peux toujours écrire f(z)=g(1/z) et si tu as un DSE de g pour |z|1/R.
Maintenant on demandait le résidu de f en 0, et j'ai donc interprété la question de Ptah Sokar à partir de ça : il me fallait un DSL sur un disque troué.

Analyse complexe

Analyse complexe

Qui est en ligne