Equations

par **challenger** » 27 Mai 2007, 17:00

Bonjour à tous,

Je suis en formation BTS par correspondance et je galère sur les maths.

J'aurais besoin vivement de votre aide pour résoudre mes 5 dernières équations qui sont à résoudre ds R

1) 5x²+ x racine carrée3 -1 = 0
2) (x+3)² = 3(2x+1)²
3) (-5x²+12x-3)/(x²-x+5) = 0
4) (-x²+x-3) / (2x²-3x-1) = 0
5) (1/(3x-2)) + (1/(-3x+1)) = 2

Merci pour votre aide

par **helene_detroie** » 27 Mai 2007, 17:06

si tu connais le discriminant, il suffit de le calculer pour avoir ta solution...
Sinon, je prends le premier par exemple:
5(x²+sqrt(3)x/5-1/5)=5[(x+sqrt(3)/10)²-3/100-1/5]=....
Pour les divisions, il suffit que le numérateur soit nul et que x ne prenne pas les valeurs interdites. Pour le dernier réduis tout au meme dénominateur

par **challenger** » 27 Mai 2007, 17:18

Merci de votre aide mais pour moi ceux - ci reste encore très vague

par **helene_detroie** » 27 Mai 2007, 17:23

Ok, je reprends....
5[(x+sqrt(3)/10)²-3/100-1/5]=5[(x+sqrt(3)/10)²-23/100). Ya plus qu'a appliquer a²-b²=(a-b)(a+b), et tu obtiens une factorisation. comme un produit est nul si et seulement si au moins un des termes est nul....
Pour le 2), tu fais passer le second membre à gauche, et tu applique la meme identité remarquable
pour la suite, tu appliques la meme methode qu'au 1) et tu vérifies que les solutions que tu obtiens n'annulent pas le dénominateur

par **julian** » 27 Mai 2007, 17:38

Bon mon "petit" challenger,
Rien que pour toi (et puisque j'ai un peu de temps devant moi), je vais te rdedonner la méthode de résolution d'équations jusqu'au 2nd degré, que tes profs ont surement déjà du t'expliquer. J'espère que ma méthode et servira, et que tu sauras l'appliquer pour de nommmmmmmmmmbreux exos.

I. Equation du type ax=b

Tu as les équations toutes bêtes qu'on rencontre dès le collège, de ce type là. Alors parfois tu pourras avoir par exemple 3x+2=5x+5, mais tu sais que tu peux les factoriser et te ramener à une équation qui a la tête de ax=b.

La solution de ces équations est:

Jusque là, y'a pas dlézards...

II. Equation du type ax²=b (vrai pour a=1 bien entendu!)

Là, il suffit de te ramener à:

Et comme je te l'ai déjà dit, il suffit de prendre

et

, car

, OK ça marche (OUF!)

III. Equation du type ax²+bx+c=0 (polynôme du 2nd degré)

Idem tu pourras avoir des équations avec des têtes un peu différentes, mais en passant les termes d'un côté de l'égalité et en factorisant ça devrait passer.
1ère étape: calculer le discriminant

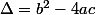
-si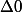

, il existe 2 racines réelles:

et

Et tu peux toujours vérifier si tes calculs sont bons. Car c'est quoi une racine? C'est un nombre qui annule ton polynome.
Donc pour vérifier, tu dois avoir:
-

si

-

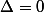
par exemple si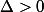

Voilà, bon courage et bonne continuation! :++:

ps: identités remarquables à savoir PAR COEUR:

par **challenger** » 27 Mai 2007, 17:51

je te remercie pour ton aide et tes conseils.

Bonne soirée

par **julian** » 27 Mai 2007, 22:25

Si ça peut te servir, y'a pas de quoi l'ami ! :++:

Bon courage!

Equations

Equations

Equation

Qui est en ligne