Difficultées avec une intégrale

par **le fouineur** » 25 Mai 2007, 16:10

Bonjour à tous,

Je me trouve bloqué sur le démarrage du calcul d'une intégrale,c'est:

Tout ce que je sais,c'est qu'il faut intégrer par parties mais je ne connais pas de primitive pour:

Merci de m'indiquer comment démarrer....

par **le fouineur** » 25 Mai 2007, 19:00

Merci Rain' pour ta réponse rapide,

En prenant u et dv tels que tu as suggéré,ça marche.Mais il faut auparavant calculer la primitive de:

....
Cordialement le fouineur

par **kinounou** » 25 Mai 2007, 19:53

Qui se trouve aussi par intégration par parties avec u= arctan et dv=x.

par **Pythales** » 26 Mai 2007, 09:59

En posant

et

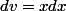
ça revient à intégrer

(facile) et

(encore plus facile)
On doit obtenir, sauf erreur

par **le fouineur** » 26 Mai 2007, 10:54

Bonjour Pythales et merci pour ta réponse,

Je suis bien arrivé au résultat que tu indiques mais par une méthode plus laborieuse:je suis passé par l'intégration de

.....
Ta remarque judicieuse me servira sans doute pour des intégrations futures...

Cordialement le fouineur

par **le fouineur** » 28 Mai 2007, 09:59

Bonjour à tous,

J'ai un nouveau problème avec l'intégrale suivante:

J'ai posé:

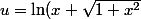donc

et dv=1 dx donc v=x et je suis bloqué sur l'intégrale de vdu car je ne vois aucune simplification apparaitre....Normalement l'intégrale de vdu vaut:

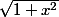
mais je ne vois pas comment....
Quelqu'un pourrait-t'il me détailler le calcul?

Merci d'avance pour vos réponses cordialement le fouineur

par **alben** » 28 Mai 2007, 10:13

Bonjour,
Ta fonction ressemble furieusement à la fonction inverse d'un sinus hyperbolique.
Avec x=sh(u), ça devrait baigner

par **alben** » 28 Mai 2007, 10:29

Au fait, il y a une erreur dans ton calcul précédent
donc

par **le fouineur** » 28 Mai 2007, 10:52

Bonjour alben,

Merci pour tes messages et le signalement de l'erreur que j'ai depuis corrigée.
N'y a t'il pas moyen de s'en sortir sans passer par les fonctions hyperboliques avec lesquelles je suis mal à l'aise? C'était un exercice sur les intégrations par parties et à priori on n'a pas le droit d'utiliser un changement de variable....

N'est-t'il pas possible de simplifier l'expression de vdu pour faire apparaitre une forme de primitive connue?

Merci de me répondre...

par **alben** » 28 Mai 2007, 10:59

Après correction de ton erreur du se simplifie en

et l'integrale de vdu ne pose pas problème

par **le fouineur** » 28 Mai 2007, 11:30

Merci alben pour ta réponse rapide,

L'expression de du se simplifie bien selon tes instructions.L'autre maladresse que j'avais faite était de multiplier tout de suite par v,ce qui compliquait les calculs....

Cordialement le fouineur

Difficultées avec une intégrale

Difficultées avec une intégrale

Qui est en ligne