salut,
J'aide actuellement la fille d'une copine qui a des difficultés en math. Du moins j'essaye.
en fait on séche sur une simplification de fraction, voici l'énoncé.
Simplifie la fraction suivante.
8X³-27
4X³-2X²-3X-18
Je sais qu'il factoriser (mais j'y arrive pas)
ensuite énoncer les conditions d'existances
et enfin simplifier.
Merci de votre aide.
cocavore.
Fractions algébriques
6 messages
- Page 1 sur 1
Une factorisation de niveau premiére :
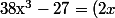^{3}-(3)^{3}=(2x-3)(4x^{2}+6x+9))
On voit ensuite que 2 est une racine évidente du polynôme au dénominateur.
On factorise soit par méthode des coefficients indeterminés soit par division polynômiale et on trouve :
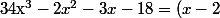(4x^{2}+6x+9))
Ainsi la fraction devient :
(4x^{2}+6x+9)}{(x-2)(4x^{2}+6x+9)})
Comme le polynôme 4x²+6x+9 ne s'annule pas sur R on peut simplifier la fraction , ce qui donne :


Jord
On voit ensuite que 2 est une racine évidente du polynôme au dénominateur.
On factorise soit par méthode des coefficients indeterminés soit par division polynômiale et on trouve :
Ainsi la fraction devient :
Comme le polynôme 4x²+6x+9 ne s'annule pas sur R on peut simplifier la fraction , ce qui donne :
Jord
Salut,
Pour effectuer la première factorisation faite par Nightmare, on commence par remarquer que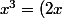^{3}) et que
et que 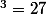 .
.
Ensuite, on applique la formule
 (a^{n-1} + a^{n-2}b + a^{n-3}b^{2} + ... + ab^{n-2} + b^{n-1}))
que l'on vérifie en constatant qu'en développant, tous les termes se téléscopent (s'annulent entre eux) sauf .
.
Ensuite, on utilise le fait que si un polynôme) a une racine
a une racine  , on peut trouver un polynôme
, on peut trouver un polynôme ) tel que
tel que =(X-a)Q(x)) .
.
:happy3:
Pour effectuer la première factorisation faite par Nightmare, on commence par remarquer que
Ensuite, on applique la formule
que l'on vérifie en constatant qu'en développant, tous les termes se téléscopent (s'annulent entre eux) sauf
Ensuite, on utilise le fait que si un polynôme
:happy3:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
