Polynome à coeff dans Z

[alex26]

Salut, je bloque sur un exercice :

Soit P un polynome unitaire à coefficients dans Z
P=X^n+sum(ak*X^k,k=1..n-1)+a0 avec a0=+1 ou -1

le polynome est scindé et toutes ses racines sont des complexes de module 1.

Mq ces racines sont des racines de l'unité.

[yos]

Si tu notes les n racines (distinctes ou non), tu as

Si k est un entier naturel, le polynôme vérifie les mêmes propriétés que P (coefs entiers, unitaire, degré n, racines de module 1).
Mais il se trouve que les coefs de ce genre de polynôme sont bornés ( est une somme de produits de racines de P donc ) et donc ces polynômes sont en nombre fini (ainsi que leurs racines du coup).
Mais on peut donner à k une infinité de valeurs donc...

[fahr451]

c'est joli ça

[redwolf]

C'est joli, mais je ne comprends pas pourquoi les coefficients des
sont entiers.

[redwolf]

Ah si !

C'est parce que tous les polynomes symétriques s'écrivent comme polynômes en les polynômes symétriques élémentaires.

Très joli en effet !

[yos]

Oui jaime beaucoup. J'ai pas utilisé le fait que le coef constant vaut 1 ou -1 (y-a-t-il plus simple avec ça?)
En tout cas c'est classique et on peut même supposer que les modules des racines de P sont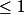 (sans changer la preuve).
Dans la littérature ça se trouve ainsi : "un entier algébrique dont tous les conjugués sont de module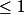 est une racine de l'unité".