Une "petite" limite...

[prody-G]

Bonjour à tous !

Je voudrais que vous m'éclairiez un peu si c'est possible pour une question ouverte ^^

On a y'= y²+1
Soit f une fonction solution de cette équation différentielle.

f est donc strictement croissante sur R

Déterminer la limite de f en +oo.

J'ai deux propositions mais je ne sais pas si elles sont bonnes :
1) Est-ce qu'une fonction strictement croissante et qui n'admet pas de tangente horizontale tend vers +oo ?

2) En passant à l'intégrale de f' de a à x avec a un réel

Voilà merci d'avance !!

[titejaune]

alors je pense que ta première idée n'est pas la bonne
car des fonctions qui n'ont pas de tangente horizontale et qui ne tendent pas vers + l'infini, ça doit se trouver assez facilement

par contre, je pense que ta deuxième idée est une bonne piste
si tu primitives la dérivée, y'a de bonnes chances que tu retombes sur la fonction, et par conséquent, après, y'a plus qu'à calculer sa limite ^^

je vais essayer
tu me diras ce que tu en penses ;-)

[titejaune]

alors si je ne me suis pas trompée, j'ai trouvé
F(x)=(1/3)x^3+x-(1/3)a^3-a
(si a est fixe, ça pose pas de problème, et ta fonction tend vers + l'infini)

par contre, je me demande
pour que ce soit la primitive, il ne faut pas que F(a)=0 ?

[prody-G]

lool c'est pour ça j'me demandais si c'était bon ou pas ^^. Merci jaune mais est-ce que tu peux me donner une fonction strictement croissante qui n'admet pas de tangente horizontale et qui ne tend pas vers +oo ?

[titejaune]

t'as raison,(j'avais lu un peu vite) ^^'
je vais chercher qd même ;-)
mais je trouve qd même que c'est moins rigoureux que la deuxième méthode
;-)

[anima]

lool c'est pour ça j'me demandais si c'était bon ou pas ^^. Merci jaune mais est-ce que tu peux me donner une fonction strictement croissante qui n'admet pas de tangente horizontale et qui ne tend pas vers +oo ?

Facile. .


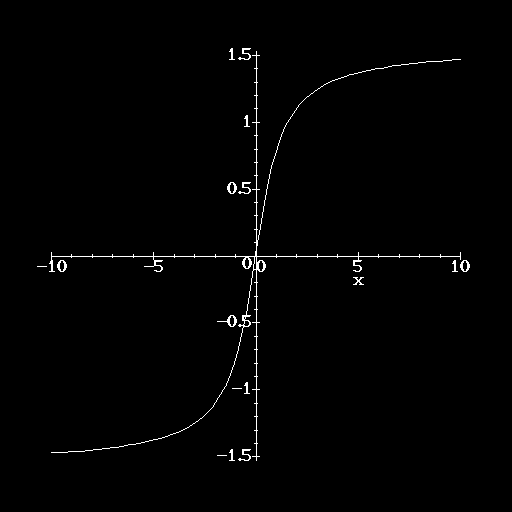
P.S: y'=y^2+1
soit y=f(x).

On integre membre-a-membre:

Et on se pose une petite tangente pour se simplifier la vie...

[prody-G]

looool chui désolé mais j'ai rien compris !
Enfin si tu le dis c'est que ça doit être vrai mais ça me paraît toujours étrange une fonction qui vérifie tout ça.

[anima]

looool chui désolé mais j'ai rien compris !
Enfin si tu le dis c'est que ça doit être vrai mais ça me paraît toujours étrange une fonction qui vérifie tout ça.

Je me suis juste contenté de te résoudre ton équation différentielle.

y'=y^2+1
y^2+1 ne s'annule jamais; on cherche donc une fonction y=f(x) définie sur R.


Tiens, je me suis planté d'un facteur 2 la premiere fois... Trop habitué a avoir des arctangentes sans dérivées en haut...

On pose une tangente pour simplifier la saloperie d'arctan

On prend = 0, tu as ta fonction: tan(x), définie sur R-{kpi} k appartenant aux entiers naturels.

[prody-G]

et elle admet pas de tangente horizontale la fonction arctan?

[anima]

et elle admet pas de tangente horizontale la fonction arctan?

Je te l'ai tracée. Si tu vois une tangente horizontale, tu me le dis...

La dérivée de la fonction arctan(u) est 1/(u^2+1). Elle ne s'annulera donc jamais...

[yos]

est-ce que tu peux me donner une fonction strictement croissante qui n'admet pas de tangente horizontale et qui ne tend pas vers +oo ?

sur R*+.
Si tu en veux une sur tout R, on peut prendre .

[anima]

sur R*+.
Si tu en veux une sur tout R, on peut prendre .

Pas d'accord, Yos. Ta premiere fonction tend vers -inf quand x->zéro...
Et pour ce qui est de la deuxieme, joli coup

[yos]

Sinon pour prouver qu'une fonction f définie sur R et vérifiant f'(t)=1+f(t)² tend vers +oo en +oo, l'idée d'intégrer de 0 à x est bonne :
on obtient d'où la limite par comparaison.
Cependant, et en vertu de la résolution d'anima, une telle fonction n'existe pas (la fonction tangente n'est pas définie sur un intervalle type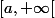 et donc on peut pas parler de sa limite en l'infini. Mais les techniques utilisées par anima sont pas au programme du lycée.

[prody-G]

ah avec celle-là je vois mieux (x--> -1/x)
Merci à vous !
en fait la fonction arctan j'l'ai jamais vue encore alors...c'est pour ça je voyais pas trop.

[yos]

Ben -1/x est strictement croissante et tend pas vers +oo en +oo. Je crois que c'est ça qui était recherché. (pour anima)

[anima]

Sinon pour prouver qu'une fonction f définie sur R et vérifiant f'(t)=1+f(t)² tend vers +oo en +oo, l'idée d'intégrer de 0 à x est bonne :
on obtient d'où la limite par comparaison.
Cependant, et en vertu de la résolution d'anima, une telle fonction n'existe pas (la fonction tangente n'est pas définie sur un intervalle type et donc on peut pas parler de sa limite en l'infini. Mais les techniques utilisées par anima sont pas au programme du lycée.

Comment expliques-tu que je suis en terminale, et que c'était au programme? Ordre 1 a coeff constants ou non-constants, ordre 2 coeffs constants :hum:

[yos]

Mais c'est pas une équation linéaire.

[anima]

Mais c'est pas une équation linéaire.

Meme. Des comme ca, j'ai du en résoudre une petite dizaine entre mars et mai... Les écoles européennes sont-elles autant en avance sur le programme Francais?

(Si oui, comment je vais m'amuser a l'oral, tiens... Correcteur venant du systeme francais. Ca va etre drole )

[prody-G]

ah bon c'est au programme les équations différentielles du second ordre ? on m'a dit qu'en terminale on se contentait des équations diff de la forme y'=ay ou y'=ay+b...

[yos]

Le programme n'interdit pas de traiter des exemples (surtout y'=1+y² où on voit tout de suite que tan est solution) mais on va pas se lancer dans des méthodes générales (d'ailleurs il n'y en a pas beaucoup).