Devoir de math
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 14 Mai 2007, 18:34
par Esenem » 14 Mai 2007, 18:34
Bonjour,
j'ai le même problème que Waaaghalex, je suis complètement bloqué!

Est-ce que quelqu'un pourrais me donner un petit coup de pouce pour me sortir de là??? Quelques pistes... Merci d'avance!

******Partie A********
1.1 La dérivée c'est bien

?
Et la dérivée seconde:

? :hein:


-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 14 Mai 2007, 18:43
par annick » 14 Mai 2007, 18:43
Bonsoir,
Ta dérivée est juste, mais je ne vois pas pourquoi tu calcules la dérivée seconde ?
Avec ta dérivée, ton tableau de variations est facile à faire et le signe de g(x) se lit directement dans le tableau.
Ensuite, sur quoi bloques-tu vraiment?
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 14 Mai 2007, 20:41
par Esenem » 14 Mai 2007, 20:41
bah sur un peu tout ^^
Donc avec la dérivée première je peux dire que la fonction est strictement croissante puisque 4e^(2x)>0 (si je ne me trompe pas)
Mais je ne vois pas ce que je peux en déduire sur le signe de g dans R :hein:
(2x-1) est négatif si x<1/2, est égal à 0 si x=1/2 et est positif si x>1/2.
e^(2x) est, je crois, toujours positif.
Et il y a ce +1...
Qui fait que:
g>0 si (2x-1)e^(2x) > -1
g=0 si (2x-1)e^(2x) = -1
g<0 si (2x-1)e^(2x) < -1
Mais bon si j'commence à regarder comme ça ce n'est plus de la déduction par rapport à la variation de g... ^^
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 14 Mai 2007, 21:38
par annick » 14 Mai 2007, 21:38
oups, j'ai lu trop vite ta dérivée, tu dois trouver 4xe^2x donc ensuite ta fonction est décroissante, puis croissante, mais toujours au dessus de 0. utilises ta calculatrice pour vérifier
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 15 Mai 2007, 06:11
par Esenem » 15 Mai 2007, 06:11
Mais comment peux-tu être sur que la fonction est toujours positive?
-
nico74
- Membre Naturel
- Messages: 63
- Enregistré le: 23 Juin 2005, 10:39
-
 par nico74 » 15 Mai 2007, 07:38
par nico74 » 15 Mai 2007, 07:38
Bonjour,
je n ai pas fait les calculs de dérivée, mais je suppose qu ils sont justes
=4xe^{2x})
.
Comme ta fonction est croissante puis décroissante, tu dois pouvoir trouver le minimum de cette fonction.
Comment faire ?

admet un minimum (ou un maximum) en

si
=0)
et

change de signe en ce point.
Ce qui est le cas ici pour

d'après le tableau de variation.
Donc

admet un minimum en

et vaut
=0)
.
Donc d'après la définition du minimum, pour tout
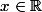
\geq 0)
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 15 Mai 2007, 16:48
par Esenem » 15 Mai 2007, 16:48

Donc,
e^{2x} \geq0)
Il faut alors que
e^{2x})
soit inférieur ou égal à 0?
Je vois qu'il y a un zéro en x=-1/2 mais comment j'peux trouver quand ce sera inférieur?
Mais sinon ton résonement me parait plus sain, je percois mieux les variations. Malgré cela, je n'arrive pas a me débloquer de l'exercice 2.1 et 2.2. Mes résultat ne sont pas propable. Une idée??
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 16 Mai 2007, 12:03
par Esenem » 16 Mai 2007, 12:03
Quelqu'un peut m'aider ??? Waaaghalex !... peut-être ...
-
yann19
- Messages: 2
- Enregistré le: 06 Mai 2007, 15:06
-
 par yann19 » 16 Mai 2007, 12:38
par yann19 » 16 Mai 2007, 12:38
salut tu recherche de l'aide à quel niveau actullement?
-
mmbelzb
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Mai 2007, 12:52
-
 par mmbelzb » 16 Mai 2007, 12:57
par mmbelzb » 16 Mai 2007, 12:57
Salut! Pour la question 2.1, c'est très simple :
calcul d'abord 1-g(x). tu trouve -(2x-1)e^2x et tu cherche à résoudre : -(2x-1)e^2x>=0
or tu sais que e^2x est toujours positif. donc tu n'a plus qu'a trouver la solution de : (2x-1)<=0
pour la question 2.2, je te conseil une intégration par partie! bonne chance!
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 16 Mai 2007, 13:29
par Esenem » 16 Mai 2007, 13:29
Oui mais le problème c'est que je n'ai pas encore vu cette méthode !
Je ne sait pas du tout comment m'y prendre :triste:
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 16 Mai 2007, 16:02
par rene38 » 16 Mai 2007, 16:02
Bonjour
2.2.




Tu dois trouver facilement une primitive de

Quant à

, tu as la réponse dans la question 1.
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 16 Mai 2007, 20:50
par Esenem » 16 Mai 2007, 20:50
Quelqu'un serait-il m'éclaircir sur la partie B ?? :cry:
-
titejaune
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Avr 2007, 18:45
-
 par titejaune » 16 Mai 2007, 21:01
par titejaune » 16 Mai 2007, 21:01
bon, alors pour la question 1
ton domaine de définition, c'est R privé de 0
donc, tu dois calculer les limites en - et + l'infini et en 0+ et 0-
ta fonction, c'est f(x) = (e^(2x)-1)/x
il faut que tu la transformes un peu afin d'obtenir une croissance comparée en plus et moins l'infini
ex : e^2x=e^x * e^x
et pour 0, tu peux faire un changement de variable, pour te retrouver avec un cas pour + l'infini, je pense que ça devrait marcher
si c'est pas clair, n'hésite pas à me le dire
;-)
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 16 Mai 2007, 21:08
par Esenem » 16 Mai 2007, 21:08
OOULLA, tous ca me parait confu, je fait une touillette, peux-tu en venir directement au faits ! Merci
-
titejaune
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Avr 2007, 18:45
-
 par titejaune » 16 Mai 2007, 21:10
par titejaune » 16 Mai 2007, 21:10
pour la question 2, je pense qu'il s'agit d'une asymptote verticale en 0
(ça s'en déduit par rapport aux limites trouvées dans la question précédente)
pour la question 3
trouver la sens de variation ...
tu as f(x)=(e^(2x)-1)/x
tu pose u(x)=e^(2x)-1
donc u'(x)=2e^(2x)
et v(x)=x
donc v'(x)=1
puis tu appliques ta formule f'(x)=[u'(x)*v(x)-u(x)*v'(x)]/(v(x)^2)
tu obtiens f'(x), tu trouves son signe, et tu peux trouver les variations de ta fonction
si y'a un pb, dis le, y'a pas de soucis ^^
-
titejaune
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Avr 2007, 18:45
-
 par titejaune » 16 Mai 2007, 21:22
par titejaune » 16 Mai 2007, 21:22
oki
je détaille un peu plus
f(x)=(e^(2x)-1)/x
on va faire sa limite en + l'infini
f(x)=(e^(2x)-1)/x=(e^x*e^x-1)/x=e^x*(e^x/x)-1/x
en plus l'infini (je n'écris pas à chaque fois les limites, mais c'est ce que je calcule), tu as donc
(e^x/x)=+ l'infini (croissance comparée)
e^x = + l'infini
par produit, tu as donc e^x*(e^x/x)=+ l'infini
1/x = 0
par somme, tu as donc lim qd x tend vers + l'infini de f(x)=+l'infini
si tu le fais en moins l'infini, c'est encore plus simple, t'as pas besoin de transformer ton expression de départ
lim e^(2x) = 0
lim -1 = -1
par somme lim e^(2x)-1=-1
divisé par - l'infini, tu obtiens zéro
-
Esenem
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Mai 2007, 15:50
-
 par Esenem » 16 Mai 2007, 21:25
par Esenem » 16 Mai 2007, 21:25
je regarde a tout ca...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités









 , tu as la réponse dans la question 1.
, tu as la réponse dans la question 1.