Inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
steef91
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Jan 2007, 21:00
-
 par steef91 » 13 Mai 2007, 10:33
par steef91 » 13 Mai 2007, 10:33
Bonjour,
J'essaie de montrer que
^k } { k!} \leq \frac { (ln2)^n } { n! })
et je n'arrive à rien de concluant... Pourtant, je pense que ca doit vraiment pas être compliqué...
Merci d'avance :++:
Steef
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 13 Mai 2007, 10:49
par tize » 13 Mai 2007, 10:49
Bonjour,
il me semble qu'une simple récurrence suffit...
-
steef91
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Jan 2007, 21:00
-
 par steef91 » 13 Mai 2007, 10:55
par steef91 » 13 Mai 2007, 10:55
Notre prof nous invite toujours à chercher autre chose que la récurrence (il a du faire un blocage dans sa plus tendre enfance...) ... Effectivement, ca doit marcher sans problème ici.
Avez vous une autre idée qu'une récurrence ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 13 Mai 2007, 11:06
par yos » 13 Mai 2007, 11:06
steef91 a écrit:Notre prof nous invite toujours à chercher autre chose que la récurrence (il a du faire un blocage dans sa plus tendre enfance...) ...
ça se soigne! Sans le raisonnement par récurrence, on peut faire aucune mathématique sérieuse (ni algèbre linéaire, ni analyse, ni arithmétique...), mais on peut faire des récurrences déguisées parfois (séries télescopiques par exemple).
Ici, je poserais
=\sum_{k\geq n+1}\frac{x^k}{k!}-\frac{x^n}{n!})
et j'étudierais le signe de la dérivée (en effet ce
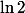
me semble décoratif. Mais j'ai pas dit que tout réel x convient!).
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Mai 2007, 11:19
par fahr451 » 13 Mai 2007, 11:19
bonjour
x = ln 2
factoriser par x^(n+1)/(n+1)! et majorer la série restante par la série géométrique de raison x/(n+1)
sauf erreur l 'inégalité est valable pour x=< (n+1) /2 donc ici n >0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités