Recherche corrigé
5 messages
- Page 1 sur 1
Recherche corrigé
Bonjour tout le monde , je recherche les corrigés de deux sujets : Le sujet du bac du liban 2006 et celui de la polynésie française 2006 . Car le bac approche à grand pas et j'aimerais pouvoir m'entrainer le plus possible . Alors si vous pouviez me dire où est-ce que je pourrais les trouver , ce serait vraiment très gentils de votre part . A bientot , bonne journée .
Bac Liban 1983
1).  etant un entier naturel , different de zero , on envisage la fonction
etant un entier naturel , different de zero , on envisage la fonction  de la variable reelle
de la variable reelle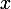 definie sur
definie sur  par
par
=x+\frac{x^2}{2} +\frac{x^3}{3} +...+\frac{x^n}{n} +\ln |x-1|)
a)Montrer que, pour tout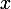 different de
different de  , on a
, on a
=\frac{x^n}{x-1})
Etudier le sens de variation de ( on distinguera les cas
( on distinguera les cas  pair et
pair et  impair ).
impair ).
Montrer que la fonction est monotone sur l'intervalle
est monotone sur l'intervalle 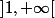 et etudier les limites de
et etudier les limites de aux bornes de cet intervalle .
aux bornes de cet intervalle .
b)Faire l'etude complete des fonctions et
et 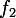 .
.
Tracer leurs representations graphiques respectives et
et  sur des feuilles distinctes.
sur des feuilles distinctes.
2.On envisage le suite) ,
,  , definie par :
, definie par :
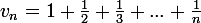
a)Montrer que est l'integrale d'une fonction constante par morceaux majorant la fonction
est l'integrale d'une fonction constante par morceaux majorant la fonction =\frac{1}{t}) sur
sur 
Etablir que1) , on a :
, on a :
>v_n+\ln (x-1)) .
.
En deduire que , pour tout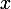 fixé strictement superieur a
fixé strictement superieur a  , on a :
, on a :
=+\infty)
4.a) Montrer que :
>v_n-\ln (n))
En deduire que) est strictement positif.
est strictement positif.
b) Montrer qu'il existe un reel unique , strictement compris entre
unique , strictement compris entre  et
et  , pour lequel
, pour lequel =0)
Verifier ce resultat sur et
et  .
.
5.a) Expliquer pourquoi on a pour tout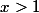 ,
,
=\int_{0}^{x} \frac{t^n}{t-1}\mathrm \, dt)
et pour ,
, =\int_{\alpha_n}^{x} \frac{t^n}{t-1}\mathrm \, dt) .
.
b) Montrer que :
|=\int_{-1}^{0} \frac{(-t)^n}{1-t}\mathrm \, dt) .
.
Montrer que pour tout entier naturel different de zero , on a :
different de zero , on a :
^n}{1-t}\mathrm \, dt \leq \int_{-1}^{0} (-t)^n \mathrm \, dt)
puis que :
| \leq \frac{1}{n+1})
En deduire que la suite)) ,
,  , est convergente et donner sa limite
, est convergente et donner sa limite
a)Montrer que, pour tout
Etudier le sens de variation de
Montrer que la fonction
b)Faire l'etude complete des fonctions
Tracer leurs representations graphiques respectives
2.On envisage le suite
a)Montrer que
Etablir que
En deduire que , pour tout
4.a) Montrer que :
En deduire que
b) Montrer qu'il existe un reel
Verifier ce resultat sur
5.a) Expliquer pourquoi on a pour tout
et pour
b) Montrer que :
Montrer que pour tout entier naturel
puis que :
En deduire que la suite
Salut, B J, ce n'est pas ce que demandais toxic, il veut les corrigés pas les sujets.
Voici un site : Voici les corrigés
Voici un site : Voici les corrigés
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
