PETIT PROBLEME (3eme)

[OfF"]

Bonjour à tous,
j'ai un problème avec un exercice de niveau 3ème.

Dans un jardin public, un bassion à la forme d'un cône.
La bordure du bassin est un cercle de rayon OC = 3 m.
Ce cercle est situé dans un plan horizontal.
La droite (OS), axe du cône, est verticale et OS = 1,2 m.


I: Quelle longueur de grillage, à 1 m près, faudra-t-il pour entourer ce bassin ? J'ai trouvé 19 mètres.
II: 1. Calculer le volume de ce bassin à 0,001m cube. J'ai trouvé V=11,310.
2. Combien de litres d'eau faudra-t-il pour remplir totalement ce bassin ?
III: 1. Quelle est la nature du triangle OSC ?
2. Calculer CS, arrondi au dm. J'ai trouvé CS = 32 dm.
3. Calculer tan ^OSC^, puis l'angle ^OSC à 1° près.

[sylvainp]

Bonsoir
Toutes tes réponses sont justes, le plus gros est fait... :lol4:
2) à savoir : 1L = 1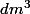 Ici tu as ou ---> fais un tableau
III 1) rectangle tout simplement vu que (OC) est perpendiculaire à (OS) "la droite (OS), axe du cône"
3) tan angle = côté opposé / côté adjacent ---> dans les triangles rectangle
donc ici : tan OSC = CO/OS = 3/1.2 = 2.5
pour trouver l'angle utilise la calculatrice.

[OfF"]

Merci beaucoup pour ta réponse. :happy2:

[OfF"]

Je pensais m'en sortir avec la suite mais j'ai encore plus de mal. :help:
J'espere que vous pourrez m'aider.



Lorsque le bassin est partiellement rempli, l'eau occupe un cône de hauteur SO' dont la base est le disque de rayon O'C'.
Le graphique ci-dessous représente les variations du volume d'eau contenue dans le bassin en fonction de la hauteur du cône d'eau.



1. Le volume d'eau est-il proportionnel à la hauteur du cône d'eau ? Justifier.

2. Par une lecture graphique, répondre aux questions suivantes:
a_ le volume d'eau étant de 1,4 m cube, quelle est la hauteur d'eau dans le bassin ?
b_ La hauteur de l'eau dans le bassin étant de 1m, quel est le volume de l'eau contenue dans le bassin ?
c_ Quelle est la hauteur du cône d'eau lorsque le volume de l'eau contenue dans le bassin est la moitié de la capacité du bassin ?

[sylvainp]

Bon allons-y
1- regarde ton graphique, il représente une courbe... et pour qu'il y est proportionalité, il faudrait que ce soit une...
2- "par lecture graphique" ---> aucun calculs
faisons le a): sur l'axe des ordonnées, tu as le volume d'eau dans le bassin de représenté, regarde pour la hauteur qui correspond.
b) même principe mais dans l'autre sens
c) cf II 1) --> capacité du bassin donc divisé par 2 égal..... puis cf a).
Demande si ce n'est pas clair

[OfF"]

1) que la variation soit droite.
2 ) J'ai 6 pour le b.
1 pour le c.
Mais j'ai pas trouvé le a.

Merci encore! :we:

[sylvainp]

1) ok mais on dira plutôt que... la représentation du volume d'eau en fonction de la hauteur du cône est une droite.
2)b et c ok et ok
pour le a logiquement si tu réussis le c le a ne pose pas problème... Quelle est la hauteur du cône correspondant à un volume de . Mais c'est vrai que l'échalle est embrouillante, 1cm -->

[OfF"]

En fesant un tableau j'ai trouvé 0,725.

Je pense pas m'être trompé.
ENCORE UN ENORME MERCI