Question de calcul ?!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 19:30
par sue » 26 Avr 2007, 19:30
bonsoir !
j'ai une tit question de calcul que je trouve un peu bizarre !
soit une fonction
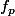
définie par :
=f(x+p))
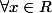
tq
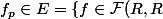\;/\; f(x)=ae^x+be^{-x} \; (a,b)\in R^2\})
bon pour mq qu'une certaine application est un morphisme..etc . on doit vérifier que :

j'ai fais le calcul de
)
et
)
chacune à part , mais j'obtiens pas l'égalité !
sinon qq chose m'échape ce soir :--:
merci d'avance !
et bonne soirée .
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 21:34
par tize » 26 Avr 2007, 21:34
Bonjour Sue,
je ne suis pas sur d'avoir compris ta question...tu veux montrer quoi exactement : qu'il existe un morphisme de quoi dans quoi ? Si c'est un morphisme de groupes quels sont les groupes et leur lois ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 21:42
par sue » 26 Avr 2007, 21:42
bonsoir Tize
je cherche à mq

merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 21:47
par tize » 26 Avr 2007, 21:47
sue a écrit:f_p définie par :
=f(x+p) \forall x\in R)
tq
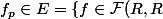\;/\; f(x)=ae^x+be^{-x} \; (a,b)\in R^2\})
Juste au cas où : c'est pas

au lieu de

?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 21:51
par sue » 26 Avr 2007, 21:51
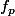
appartient à E , selon sa définition :
=f(x+p))
je ne vois pas le prob. :hein:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 21:55
par tize » 26 Avr 2007, 21:55
sue a écrit: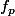
appartient à E , selon sa définition :
=f(x+p))
je ne vois pas le prob. :hein:
Je veux bien définir f_p par :
=f(x+p))
mais dans ce cas, qui est f ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 21:58
par sue » 26 Avr 2007, 21:58
f est définie par :
=ae^x+be^{-x})
\in R^2)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 22:04
par tize » 26 Avr 2007, 22:04
OK, j'ai compris. Merci
mais la relation

me semble fausse : on a a gauche une combinaison d'exponentielle et à droite une combinaison de composées d'exponentielle !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 22:14
par sue » 26 Avr 2007, 22:14
ah ben oui c'est exactement ce que je vois moi !
mais c'est vraiment trés bizarre car je l'ai eu ce matin dans mon bac blanc et les questions suivante reposent sur celle là .
on demande de prouver que l'application

: R -- E tq :
=f_p)
est un automorphisme de (R,+) -- (E,o)
puis en déduire la structure de (E,o) et ses élément caractéristiques !
bon moi j'ai considéré l'égalité vrai et j'ai fait le reste lol .
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 22:21
par tize » 26 Avr 2007, 22:21
Plutôt troublant..., es-tu sur qu'ils ont utilisé le terme "automorphisme" de (R,+) --> (E,o), car un automorphisme est un endomorphisme et

n'en est clairement pas un !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 22:25
par sue » 26 Avr 2007, 22:25
ben je peux me tromper pour le terme mais un automorphisme , n'est-il pas un homomorphisme bijectif ? (c'est la traduction exacte)
-
Ted
- Membre Naturel
- Messages: 71
- Enregistré le: 26 Mar 2007, 21:22
-
 par Ted » 26 Avr 2007, 22:30
par Ted » 26 Avr 2007, 22:30
en fait la quuestion est tres tordue
(Fp)o(Fq)(x)= (Fp)[f(x+q)]=f((x+q)+p)=f(x+q+p)=Fp+q(x)
Ne pas confondre les Fp avec les f!!!
En relisant l'énnoncé c'est vrai que ma réponse colle pas trop, mais c'est comme ça que je connais cet exercice
ensuite un morphisme bijectif s'appelle un isomorphisme à ma connaissance
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 22:35
par sue » 26 Avr 2007, 22:35
(Fp)[f(x+q)]=f((x+q)+p)=
je ne suis pas tt à fait d'accord là : Fp[f(x+q)] = f(f(x+q)+p) nan?
OK pour isomorphisme , je le confond tj avec automorphisme , merci !
-
Ted
- Membre Naturel
- Messages: 71
- Enregistré le: 26 Mar 2007, 21:22
-
 par Ted » 26 Avr 2007, 22:38
par Ted » 26 Avr 2007, 22:38
C'est tout le problème en fait...
J'ai répondu un peu vite parceque j'ai déjà vu cet exercice
et c'est vrai que cette réponse colle pas trop à ton énoncé.
Mais je vois pas trop comment y arriver en utilisant la composition classique.
Essaye de voir avec une calculatrice si tu as une égalité pour quelques valeurs mais ça m'étonnerais fort.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 22:38
par tize » 26 Avr 2007, 22:38
sue a écrit:ben je peux me tromper pour le terme mais un automorphisme , n'est-il pas un homomorphisme bijectif ? (c'est la traduction exacte)
automorphisme = endomorphisme bijectif
isomorphisme = homomorphisme bijectif
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 22:56
par sue » 26 Avr 2007, 22:56
ok, tize merci !
sinon Ted , j'ai essayé avec des valeurs et ça marche pas !
comment ose-t-on poser une telle question dans un bac blanc :briques:
elle m'a troublé un tit peu pendant l'examen mais j'ai laissé tomber 'heureusement' !
-
Ted
- Membre Naturel
- Messages: 71
- Enregistré le: 26 Mar 2007, 21:22
-
 par Ted » 26 Avr 2007, 23:00
par Ted » 26 Avr 2007, 23:00
Tu as directement recopier le sujet depuis ta feuille ou tu nous le ressors de tête?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 26 Avr 2007, 23:03
par sue » 26 Avr 2007, 23:03
directement de ma feuille !
-
Ted
- Membre Naturel
- Messages: 71
- Enregistré le: 26 Mar 2007, 21:22
-
 par Ted » 26 Avr 2007, 23:17
par Ted » 26 Avr 2007, 23:17
Soit il y a erreur d'énoncé, soit on interprete mal...
Y avait-il des question avant sur le même exercice?
Tu cherches quel genre de morphisme? un morphisme de groupe? une application linéaire?
n'as tu pas confondu (E,o) avec (E,+)?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 23:18
par tize » 26 Avr 2007, 23:18
Ted a écrit:Soit il y a erreur d'énoncé, soit on interprete mal...
Y avait-il des question avant sur le même exercice?
Tu cherches quel genre de morphisme? un morphisme de groupe? une application linéaire?
n'as tu pas confondu (E,o) avec (E,+)?
Oui, je me pose les mêmes questions...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
