Justement, dans mes références, je n'ai jamais vu
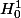
écrit comme ça.
Quand je disais que je comprenais très bien de quoi tu parlais, c'est justement car je sais aussi qu'en gros dans
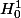
on parle de fonctions qui s'annulent au bord. Mais c'est justement le "en gros" qui nous pose problème et qui j'en suis sûr te pose problème au vu de ta question.
D'ailleurs les exemples de serge sont très justes et montre bien la limite de cette définition car se sont bien des contre-exemples qu'il nous a donné.
Je te donne ce que je sais de source sûre:
1) dans
)
tout court on sait que chaque classe de fonction peut être représentée par une fonction
)
. On ne sait rien pour l'instant sur l'annulation au bord.
2)
)
sont les fonctions
)
à support compact. Pour elles, on est d'accord qu'elles s'annulent au bord. C'est pour ça qu'elles sont construites.
3) par contre, pour moi
)
ce n'est rien d'autre que la fermeture de
)
dans
)
.
Autrement dit, pour toute fonction u de
)
, il existe une suite (fn) de fonctions dans
)
qui converge vers u pour la norme de
)
.
on dit donc des fonctions u de
)
qu'elles satisfont u=0 sur le bord au "sens faible"
"en gros" elles sont très proches de fonctions qui s'annulent au bord.
Je ne pense pas que cela veut dire qu'elle s'annulent au bord tout court!
4) je connais un théorème qui dit:
si u est dans
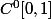
avec u(0)=u(1)=0 et u restreint à ]0,1[ est dans
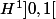
,
alors, u est dans de
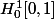
.
Par contre toi tu veux en quelques sorte prouver la réciproque.
Cette réciproque je ne la connait pas.
Alors le raisonnement serait le suivant: si tu prends une fonction de
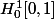
avec ma définition 3) et que tu prouve que la classe de cette fonction dans

peut être représenté presque partout par une fonction u dans
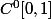
avec u(0)=u(1)=0 et u restreint à ]0,1[ dans
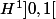
alors il y a égalité entre
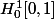
et l'ensemble de ces fonctions u.
et j'écrirais:
avec u une fonction et [u] sa classe dans

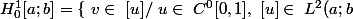 ,\ [u'] \in\ L^2(a;b) et u(a)=u(b) = 0 \}\)
et seulement après cela, avec une grande, grande précaution et que tout est clairement définit on pourrait écrire
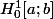
comme tu le fais.
Si ton fameux théorème est cette réciproque, tu as ton explication.
La définition que tu as n'est pas celle que l'on donne directement. Celle que l'on donne directement est la mienne. Pour que la tienne viennent coincider avec la mienne et bien... il faut montrer que c'est la même chose.
D'ailleurs je pense que ta définition n'est pas valable sur n'importe quel espace, ça ne peut donc pas etre la définition de base!
Il n'y a donc pas de problème d'ecriture à proprement parler, mais certainement un problème de cohérence avec ce qui a était écrit avant sur ton ouvrage.
