Topologie

[road runner]

bonsoir a tous
comment montrer que (X,T) est un espace topologique :

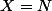
(ensemble des entiers naturel)
et
et puis comment determiner tous les fermés de (X,T)?

merci d'avance

[Ted]

Si T c'est bien ta définition des ouverts,
les fermés sont les complémentaires des ouverts, donc cherche les complémentaires des ouverts U de T.

[road runner]

merci de ton aide
mais comment montrer que le couple (X,T) forme un espace topologique?

[Ted]

Pardon je n'avais pas vu la première question:
en fait les ouverts, c'est à dire les élément de T doivent vérifié certaines propriétés, si mes souvenirs sont bons on doit montrer par exemple que l'intersection de deux elements de T reste dans T et quelques autre propriétés dans le genre

[road runner]

oui je sais c'est les axiomes de Hausdorff
mais je n'y arrive pas avec cette exercice la
toute aide est la bienvenue

[Ted]

En fait j'ai aussi un problème pour voir que N tout entier est ouvert, sinon pour le reste

1) l'ensemble vide est dans T (c'est écrit d'ssus)

2) une réunion (même) infinie d'ouvert est un ouvert
regarde un peu la réunion de seulement 2 ouverts et tu verras comment simplifier l'affaire. Le seul problème est pour l'intersection infinie d'ouverts de plus en plus grands

3) l'intersection de deux ouverts est ouverte, Prends toi deux ouverts et regarde l'intersection.

C'est tellement simple que je ne vois pas comment t'aider.

As-tu quand même vu à quoi ressemblaient les elements de T?

[yos]

Bonsoir.
Tu dois montrer que T contient X et , puis que T est stable par réunion quelconque et par intersection finie.
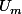
Par exemple l'intersection de et de est .
Pour une réunion c'est pas plus difficile.
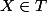
Cependant, le fait que ne m'apparait pas.

[road runner]

ils sont du genre {n,n+1,n+2..........}
c'est bien ca ?

[yos]

ils sont du genre {n,n+1,n+2..........}
c'est bien ca ?

T'es sûr d'avoir mis l'inégalité dans le bon sens dans ton premier message?

[nuage]

Salut,
il me semble qu'il y a un problème :
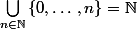
une union quelconque d'ouvert est un ouvert or n'est pas de la forme donnée pour les ouverts car n'est pas majoré.

[road runner]

je me suis trompé
c'est SUPERIEUR ou EGALE
desole

[Ted]

oui c'est ça.
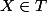
Par contre comme yos a le même problème que moi pour trouver regarde si tu ne t'es pas trompé sur ton énnoncé.
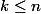
est-ce bien et pas l'inverse?
n'as tu pas directement oublié directement N dans la définition de T?

[yos]

je me suis trompé
c'est SUPERIEUR ou EGALE
desole

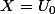
Alors c'est bon , mais du coup faut changer :

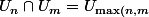[road runner]

et pour l'intersection

[yos]

et pour l'intersection

Ben c'est ce que j'ai fait.

[road runner]

c'est bon merci a tous

[road runner]

bonsoir ,
quels sont les fermes de T ? j'ai pense aux complementiares de U ,ca me donne U= { k < n} ?
ensuite je dois determiner l'aderence de N* ,je trouve que c'est vide ?
puis on me dit :soit une partie A de X ,je dois determiner son adherence ainsi que son interieur et quelle sont les partie dense de X et d'en deuire les partie d'interieur vide de X ,et la je sais pas comment faire

merci de confirmer mes reponses et de m'aider un peu

[road runner]

alors ,comment je fais ?

[road runner]

juste comment faire ,svp.

[cyberchand]

Oui avec >= c'est mieux :) donc l'intersection finie : que vaut intersection des {n >= k_i}, avec i entre 1 et K? Tu dois voir apparaitre le max des k_i.
Même question pour une réunion quelconque de {n >= k_i}. Tu dois voir apparaitre le min.
La raison pour laquelle l'intersection doit être finie et pas la réunion, est qu'on peut prendre le min d'un nombre quelconques d'entiers, mais on ne peut pas prendre le max d'un nombre infini (tous distincts) d'entiers.