Bonjour j'aimerais démontrer la chose suivante :
On a P appartenant à C[X] et P différent de 0 de degrés de P égal n
Comment montrer que la famille (P,P',P'',P'''.....P^(n)) est libre ?
(où P désigne un polynome)
Algébre linéaire
5 messages
- Page 1 sur 1
salut,
tu veux peut etre que je développe un peu la réponse expéditive de joker?
Tu ecris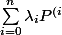}=0) (polynôme nul) (première chose à faire pour montrer qu'une famille est libre).
(polynôme nul) (première chose à faire pour montrer qu'une famille est libre).
Un polynôme est nul ssi tous ses coefs sont nuls, donc en particulier le coefficient de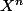 qui n'est autre que
qui n'est autre que  , puisque seul P possède un terme de degré n. Or
, puisque seul P possède un terme de degré n. Or  est non nul, donc
est non nul, donc 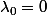 .
.
Tu obtiens donc}=0) . Le seul terme de degré (n-1) est
. Le seul terme de degré (n-1) est  . Le même raisonnement te donne donc
. Le même raisonnement te donne donc 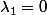 , etc...
, etc...
tu veux peut etre que je développe un peu la réponse expéditive de joker?
Tu ecris
Un polynôme est nul ssi tous ses coefs sont nuls, donc en particulier le coefficient de
Tu obtiens donc
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
