Topic à supprimer dsl
14 messages
- Page 1 sur 1
Attend, reprenons ma question :
Modélisation par une fonction f définie par f(x)=250+Be^(Ax) :
On pose zi=ln(yi-250)
Déterminer une équation de la droite de régression par la méthode des moindres carrés de z en x de la série (xi,zi). Selon ce modele quelle teneur en CO2 peut-on prévoir pour 2010 ? y: 0,001x+3,2 et donc on remplace x par 160 (nombre qui correspod au rang de l'année 2010) et on trouve 3,37 !
Jusqu'ici pas de probleme j'ai tout fait.
C'est la que ça se corsse... :
Placer le point N correspondant à cette prévision. Je ne vois pas comment on peut placer un 3,4 par exemple dans un repere qui commence par 250 en ordonnée..c'est pas cohérent pour moi... Vous trouver quoi vous ?
Voilà, je pense que l'on doit déterminer l'équation par rapport à [COLOR=Red]zi (enfin je pense) Non ?[/COLOR]
Modélisation par une fonction f définie par f(x)=250+Be^(Ax) :
On pose zi=ln(yi-250)
Déterminer une équation de la droite de régression par la méthode des moindres carrés de z en x de la série (xi,zi). Selon ce modele quelle teneur en CO2 peut-on prévoir pour 2010 ? y: 0,001x+3,2 et donc on remplace x par 160 (nombre qui correspod au rang de l'année 2010) et on trouve 3,37 !
Jusqu'ici pas de probleme j'ai tout fait.
C'est la que ça se corsse... :
Placer le point N correspondant à cette prévision. Je ne vois pas comment on peut placer un 3,4 par exemple dans un repere qui commence par 250 en ordonnée..c'est pas cohérent pour moi... Vous trouver quoi vous ?
Voilà, je pense que l'on doit déterminer l'équation par rapport à [COLOR=Red]zi (enfin je pense) Non ?[/COLOR]
Quelques points de désaccord :
moi je trouve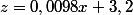
J'en déduit pour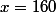 que
que 
Une fois déterminé z il reste a calcucer) en utilisant
en utilisant -250 =\ln(z)) d'où
d'où = 250 + \text{e}^z) et
et \simeq 250+\text{e}^{4,78}\simeq 370)
Voilà mon avis
A+
martineza a écrit:Attend, reprenons ma question :
Modélisation par une fonction f définie par f(x)=250+Be^(Ax) :
On pose zi=ln(yi-250)
Déterminer une équation de la droite de régression par la méthode des moindres carrés de z en x de la série (xi,zi). Selon ce modele quelle teneur en CO2 peut-on prévoir pour 2010 ? y: 0,001x+3,2 et donc on remplace x par 160 (nombre qui correspod au rang de l'année 2010) et on trouve 3,37 !
Jusqu'ici pas de probleme j'ai tout fait.[/
moi je trouve
J'en déduit pour
martineza a écrit:C'est la que ça se corsse... :
Placer le point N correspondant à cette prévision. Je ne vois pas comment on peut placer un 3,4 par exemple dans un repere qui commence par 250 en ordonnée..c'est pas cohérent pour moi... Vous trouver quoi vous ?
Voilà, je pense que l'on doit déterminer l'équation par rapport à [COLOR=Red]zi (enfin je pense) Non ?[/COLOR]
Une fois déterminé z il reste a calcucer
Voilà mon avis
A+
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
