Bonjour, j'ai un exercice de probabilité à faire et je bloque sur une généralisation.
Voici l'énoncé:
On dispose de d boules rouges et de d boules vertes qui sont réparties au départ entre 2 urnes U1 et U2. Chaque urne contient d boules après ce partage.
On répète l'expérience consistant à choisir simultanément une boule dans chaque urne et à la changer d'urne.
On appelle Xn le nombre de boules rouges après n expériences dans l'urne U1.
I) Dans cette partie toutes les boules rouges sont placées au départ dans U2, donc Xo=0 et X1=1.
2°) Exprimer P(Xn=i) en fonction de P(Xn-1=0), P(Xn-1=1),.....,P(Xn-1=d).
Merci d'avance
Exercice Probas
5 messages
- Page 1 sur 1
Salut,
Pour avoir i boules rouges dans U1 (0<i<d) il y a trois cas possibles
-a- Il y en avait déjas i et on a échangé deux boules de même couleur.
-b- Il y en avai i-1 et on a pris une boule rouge dans U2 une verte dans U1
-c- il y en avai i+1 et on a pris une boule rouge dans U1 une verte dans U2.
On peut remarquer que le nombre de boules vertes dans U2 est égal au nombre de boules rouges dans U1.
Pour le cas -a- la proba d'avoir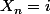 sachant que
sachant que 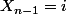 est
est 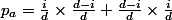
Je te laisse traiter les cas -b- et -c- ainsi que i=0 et i=d.
Si tu as trop de mal redemande.
A+
[modification] ps : avec les notations précédentes
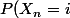=p_a P(x_{n-1}=i)+p_b P(x_{n-1}=i-1)+p_c P(x_{n-1}=i+1))
Pour avoir i boules rouges dans U1 (0<i<d) il y a trois cas possibles
-a- Il y en avait déjas i et on a échangé deux boules de même couleur.
-b- Il y en avai i-1 et on a pris une boule rouge dans U2 une verte dans U1
-c- il y en avai i+1 et on a pris une boule rouge dans U1 une verte dans U2.
On peut remarquer que le nombre de boules vertes dans U2 est égal au nombre de boules rouges dans U1.
Pour le cas -a- la proba d'avoir
Je te laisse traiter les cas -b- et -c- ainsi que i=0 et i=d.
Si tu as trop de mal redemande.
A+
[modification] ps : avec les notations précédentes
J'aurai encore une question.
Toujours dans ce même exercice (c'est un DM), j'ai une nouvelle situation:
On dispose de d boules rouges et de d boules vertes qui sont réparties au départ entre 2 urnes U1 et U2. Chaque urne contient d boules après ce partage.
On répète l'expérience consistant à choisir simultanément une boule dans chaque urne et à la changer d'urne.
On appelle Xn le nombre de boules rouges après n expériences dans l'urne U1.
II)"Dans cette partie on prend les d boules rouges une par une et on les place indifféremment dans U1 ou U2. On complète avec les boules vertes pour avoir 2 urnes de même contenance. Xo est le nombre de boules rouges dans U1. Déterminer le loi de Xo."
Doit on travailler avec des combinaisons ? Je ne comprends pas très bien l'énoncé en réalité.
Pour le moment, ma seule idée est, pour le numérateur:
P(Xo=i) = 0.5*d+0.5²d(d-1)+0.5^3*d(d-1)(d-2) +...+0.5*i*(d(d-1)....(d-i+1)
Mais je n'ai aucune conviction!
Merci d'avance
Toujours dans ce même exercice (c'est un DM), j'ai une nouvelle situation:
On dispose de d boules rouges et de d boules vertes qui sont réparties au départ entre 2 urnes U1 et U2. Chaque urne contient d boules après ce partage.
On répète l'expérience consistant à choisir simultanément une boule dans chaque urne et à la changer d'urne.
On appelle Xn le nombre de boules rouges après n expériences dans l'urne U1.
II)"Dans cette partie on prend les d boules rouges une par une et on les place indifféremment dans U1 ou U2. On complète avec les boules vertes pour avoir 2 urnes de même contenance. Xo est le nombre de boules rouges dans U1. Déterminer le loi de Xo."
Doit on travailler avec des combinaisons ? Je ne comprends pas très bien l'énoncé en réalité.
Pour le moment, ma seule idée est, pour le numérateur:
P(Xo=i) = 0.5*d+0.5²d(d-1)+0.5^3*d(d-1)(d-2) +...+0.5*i*(d(d-1)....(d-i+1)
Mais je n'ai aucune conviction!
Merci d'avance
Salut,
Je dirais que chacune des d boules rouges à une proba constante (1/2) de se retrouver dans U1. De plus il semble que les choix successifs soient indépendants.
Ce qui évoque une loi binomiale (si tu connais). Sinon pour avoir i boules rouges dans U1 il faut d'abord choisir les i boules qui seront dans U1 et il y a 2^n répartitions possibles (nombres d'applications d'un ensemble à d éléments dans un ensemble à 2 éléments) .
A+
Je dirais que chacune des d boules rouges à une proba constante (1/2) de se retrouver dans U1. De plus il semble que les choix successifs soient indépendants.
Ce qui évoque une loi binomiale (si tu connais). Sinon pour avoir i boules rouges dans U1 il faut d'abord choisir les i boules qui seront dans U1 et il y a 2^n répartitions possibles (nombres d'applications d'un ensemble à d éléments dans un ensemble à 2 éléments) .
A+
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
