Equation différentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Juls121
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Avr 2006, 14:18
-
 par Juls121 » 19 Avr 2007, 12:46
par Juls121 » 19 Avr 2007, 12:46
personne ne sait faire ca? parceque j'ai beau relire mon cours je ne vois pas comment faire.
Je dois remplacer y'-3y de (E) par ce que j'ai trouvé dans la question 2?
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 13:11
par allomomo » 19 Avr 2007, 13:11
Salut,
f est le produitde deux fontions dérivables ... tu dérives ...
-
Juls121
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Avr 2006, 14:18
-
 par Juls121 » 19 Avr 2007, 13:20
par Juls121 » 19 Avr 2007, 13:20
allomomo a écrit: f est le produitde deux fontions dérivables ... tu dérives ...
oui oui j'ai fait cette question, je trouve q'(x)-3q(x)= f'(x)/exp(-3x)
(j'ai mis un q à laplace du phi)
c'est pour la question d'apres que je bloque
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 13:23
par allomomo » 19 Avr 2007, 13:23
Salut,
Ecrit ce que ca vaut dire :

est solution de
)
ssi elle vérifie
-3\varph(x)=f'(x)e^{3x} = -\frac{3e}{\Big(1+e^{-3x}\Big)^2})
Donc
=e\times \frac{-3e^{-3x}}{\Big(1+e^{-3x}\Big)^2})
et donc
=\int f'(x)dx=e \int \frac{-3e^{-3x}}{\Big(1+e^{-3x}\Big)^2} dx=e\int\frac{u'}{u^n}dx=-\frac{e}{1+e^{-3x}}+c, c\in\bb{R})
et pour finir : Pour

on a
=\frac{e}{2})
Voila c'est fini.
-
Juls121
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Avr 2006, 14:18
-
 par Juls121 » 19 Avr 2007, 13:31
par Juls121 » 19 Avr 2007, 13:31
allomomo a écrit:-3\varph(x)=f'(x)e^{3x} & = & -\frac{3e}{\Big(1+e^{-3x}\Big)^2}<br />\end{eqnarray})
Oui j'ai pensé à ca, mais je vois pas trop comment faire après. On me demande de déterminer f, or avec la question d'avant j'ai f'. Je dois exprimer f' et primitiver?ou alors je comprends mal la question :s
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 13:36
par allomomo » 19 Avr 2007, 13:36
En haut .. :) tout y est.
-
Juls121
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Avr 2006, 14:18
-
 par Juls121 » 19 Avr 2007, 13:39
par Juls121 » 19 Avr 2007, 13:39
allomomo a écrit:Salut,
Ecrit ce que ca vaut dire :
-3\varph(x)=f'(x)<span style=)
/e^{3x} = -\frac{3e}{\Big(1+e^{-3x}\Big)^2}"/>
juste un petit détail, je trouve un diviser moi en rouge?
EDIT nan j'ai rien dit j'avais mal lu ce que tu avais marqué! merci pour ton aide:)
EDIT2 oui je venais de m'en rendre compte^^
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 13:42
par allomomo » 19 Avr 2007, 13:42
Re -
J'ai changé le signe à l'intérieur de l'exp...
Parce que :
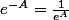
non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
