Norme d'un opérateur

[Moumni]

Salut tout le monde du forum:

Etant donné deux espaces de Banach X et Y dont les normes sont notées respactivement et et T un opérateur borné de X dans Y.
La norme de T est par définition:
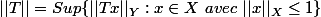
Ma question est:
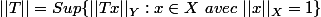
Pourquoi la norme de l'opérateur T peut etre aussi défini de l'une des manières suivantes: ou encore

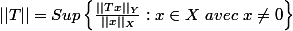
En d'autre terme : Pourquoi les trois définitions précedantes sont équivalentes?
et merci bien pour votre aide
Amicalement Moumni

[Anonyme]

soit n1=sup pour ||x|| <= 1, n2=sup pour ||x||=1 et n3=sup ||Tx||/||x|| pour x non nul.
On a evidmt n2<=n1
si x n'est pas nul, ||Tx||=||x||*||T(x/||x||)||, donc n1<=n2 d'ou la premiere egalité.
si ||x||=1 alors ||Tx||=||Tx||/||x|| donc n2<=n3
enfin en divisant en ht et en bas par ||x|| on obtient n3<=n2