Série/intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dimi
- Messages: 6
- Enregistré le: 14 Avr 2007, 13:52
-
 par dimi » 14 Avr 2007, 13:57
par dimi » 14 Avr 2007, 13:57
Bonjour,
j'aurai besoin d'aide pour démarrer un exercice


J'ai calculé I0 et I1 sans problème
I0 = pi/4
I1 = ln(2)/2
mais apres je bloque je ne comprend pas comment commencer la question 2
Merci de votre aide
-
dimi
- Messages: 6
- Enregistré le: 14 Avr 2007, 13:52
-
 par dimi » 14 Avr 2007, 14:02
par dimi » 14 Avr 2007, 14:02
Je vais chercher de ce coté la alors :)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Avr 2007, 14:03
par yos » 14 Avr 2007, 14:03
Bonjour.
On peut aussi reconnaître une forme
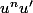
dans l'intégrale
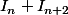
.
Pour la suite : "en déduire

", c'est mal posé.
-
dimi
- Messages: 6
- Enregistré le: 14 Avr 2007, 13:52
-
 par dimi » 14 Avr 2007, 14:18
par dimi » 14 Avr 2007, 14:18
Je ne vois pas la forme

dans

!
Est ce que tu peux m'éclairer un peu ?

-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Avr 2007, 14:20
par yos » 14 Avr 2007, 14:20
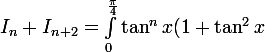dx)
.
Quelle est la dérivée de tan ?
-
buzard
- Membre Relatif
- Messages: 274
- Enregistré le: 22 Mai 2006, 14:29
-
 par buzard » 14 Avr 2007, 15:02
par buzard » 14 Avr 2007, 15:02
et avec un changement de variable t=tan(x/2), t'as essayé?

c'est un peu bourin j'en conviens mais ça doit marcher.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Avr 2007, 15:18
par fahr451 » 14 Avr 2007, 15:18
yos a tout dit (comme toujours?) surtout pas passer en t = tan(x/2)
tan ' = en fonction de tan
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 14 Avr 2007, 16:22
par allomomo » 14 Avr 2007, 16:22
Salut,
En plus * Ta série converge. voir comment le démontrer
ici, cherchez : 'harmonique'
* Et aussi :
^n}{n+1}=\sum_{n=0}^{+\infty}\frac{cos(n\pi)}{n+1}\longrightarrow ln2)
[center]

[/center]
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Avr 2007, 17:18
par yos » 14 Avr 2007, 17:18
fahr451 a écrit:yos a tout dit (comme toujours?)
Merci Fahr (en dehors du point d'interrogation).
Je continue quand même : la convergence de la série est évidente avec le th des séries alternées mais c'est pas utile d'en parler car on veut la somme. Et ça c'est pas tout à fait évident d'ailleurs.
La relation
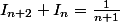
donne, après avoir posé
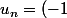^nI_{2n+1})
:
^n}{2(n+1)})
,
d'où le résultat en sommant de 0 à N puis en faisant tendre N vers l'infini.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Avr 2007, 17:56
par fahr451 » 14 Avr 2007, 17:56
sans le point d 'interrogation ça faisait flagornerie
-
dimi
- Messages: 6
- Enregistré le: 14 Avr 2007, 13:52
-
 par dimi » 15 Avr 2007, 15:05
par dimi » 15 Avr 2007, 15:05
Rebonjour
Dans l'ennoncé quand il dise "en deduire In" qu'est ce qu'il faut faire exactement ? je ne comprend pas la question :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
