Calcul d'erreur

[natacha51]

bonjour,
jai un souci pour un calcul d'erreur:

[COLOR=Green]un phénomène de croissance bactériene pet etre décrit en fonction du temps t par la relation:

N(t) = No x exp (kt)

où N(t) mesure le nombre de bactéries au temps t et k est une constante positive

sachant que l'on commet une erreur delta t sur t, delta n sur n(t) et delta No sur o, calculer l'expression littérale résultante delta k sur k[/COLOR]

merci de vos réponses!

[nuage]

Salut,
on a .

On a donc (relation que je suppose connue).

Reste à calculer
Pour ceci on utilise la dérivée de la fonction ln : soit .

Et je te laisse continuer...

[natacha51]

merci pour ton aide

[mathelot]

bonjour nuage,
distingue tu entre erreur algébrique et erreur absolue:
en d'autres termes:




ou



Quelle formule prend on pour évaluer l'erreur sur un quotient ? Dans la
première formule, on admet que les erreurs peuvent parfois se compenser,
ce qui n'est pas le cas dans la seconde formule.

[nuage]

Salut,
Dans le cadre d'un calcul d'erreurs on utilise la 2° formule que tu as donnés. En fait on calcule un majorant approché de l'erreur.
Pour pouvoir utiliser le fait que les erreurs se compensent il faudrait :
- soit connaitre leurs signes (ce qui permet normalement de réduire l'erreur)
-soit faire une étude probabiliste (mais c'est plus difficile et assez long)

Une dernière remarque : on suppose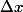 petit et aussi

[mathelot]

Bonjour,

Pour l'approche probabiliste, on étudie la loi de l'erreur et on remplace l'erreur par son espérance ?

Cordialement,

[nuage]

Salut,
En principe l'espérance de l'erreur est nulle.
On peut sans doute s'intéresser à l'espérance de la valeur absolue, mais ça je connais pas.
En général on suppose que l'on a des v.a. normales pour les erreurs et on cherche à estimer la loi du résultat et son écart-type.

A+