Dérivées partielles pour fonctions composées

[Elymel]

Bonjour a tous !
Voila mon probleme, j'ai l'égalité suivante :
f(x,y)=g(x,y+h(x,y))

Je souhaite en déduire une égalité en utilisant les derivées partielles de ces fonctions...
Pouvez-vous m'aider ?
Merci bien :)

[Ted]

Quelle genre d'egalité veux-tu obtenir?
en dérivant on peut en deduire à peu pres tout et n'importe quoi...
A moins que tu ne veuille juste deriver f.

[buzard]

bonjour,

tu parle certainement des formules de dérivation lors des changements de variables.


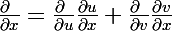
après tu adapte, cordialement

[Elymel]

En fait, est-il possible de dériver par rapport à x de chaque coté ? A ce moment là, le terme de gauche que devient-t-il ? De même pour deriver par rapport à y

[fahr451]

bonsoir oui

df/dx = dg/dx + dh/dx dg/dy

[Ted]

J'ecrirais plutot avec u=x et v=y+h(x,y):

df/dx(x,y)=dg/du (u,v)+dh/dx (x,y)*dg/dv (u,v)

[fahr451]

et tu aurais sans doute bien raison de ne pas mélanger les variables du moins au début mais quand on sait de quoi on cause ce n'est pas un problème

[Ted]

Je ne doute pas que tu savais de quoi tu parlais, mais le but de l'exercice est, je pense, de ne pas melanger les ecritures.
D'ailleurs plus je regarde, plus je me dis que mon dg/du n'est pas plus exempt de reproche que ton dg/dx.

[fahr451]

ah ben alors on a un éternel insatisafait
alors que moi un rien me contente

[Elymel]

Merci beaucoup ! Justement mon gros probleme est le suivant : derive-t-on par y ou bien par v=y+h(x,y) ?
Si jamais il faut deriver par v, comment fait-t-on alors pour deriver par v ?


QQues explications pour m'eclairer serait apreciable :)

En tous cas merci beaucoup

[serge75]

Ce n'est qu'une question de convention elymel ; pour ne pas se mélanger on appelle dg/du et dg/dv les dérivées partielles de g. Mais il faut n'y voir qu'une notation.
De même on va poser u(x,y)=x et v(x,y)=y+h(x,y), mais ces u et v là qui sont des fonctions n'ont rien à voir (mathématiquement du moins) avec les u et v de dg/du et dg/dv qui sont eux des notations; il n'empêche que moyennant ces écritures cela permet d'écrire df/dx=du/dx.dg/du+...