Aux probabilistes confirmés

[sexapil64]

Un scribe doit copier n pages d'un manuscrit. Comme il est fatigué, il comet un nombre total d'erreurs distribuées à distribution de Poisson Po(lambda), qui peuvent se trouver sur n'importe quelle page, avec des probabilités égales. Quelle est l'esperance du nombre des pages contenant des erreurs ?

je suis en galere, si quelqu'un peut m'aider, je vous remercie

[serge75]

En gros tu veux l'espérance de la loi de Poisson ? Regarde dans ton cours, elle doit figurer.

[sexapil64]

Ben si ce n'était que ca, c'est plutot évident :)
meme moi je sais ce que c'est, mais ca doit etre beaucoup plus complexe que ca :)

[nuage]

Salut,
La somme de deux v.a. suivant des lois de Poisson indépendantes suit une loi de Poisson. Son paramètre est la somme des paramètres.
Dans ton problème on peut considérer que le nombre d'erreurs par page suit une loi de Poisson de paramètre .
On peut ensuite considérer la v.a. qui vaut 0 si il n'y a pas d'erreur sur la page, proba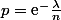 et 1 si il y a au moins une errreur, proba .

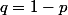Je te laisse continuer.

[sexapil64]

merci beaucoup beaucoup :we:

[fahr451]

bonjour
soit Y le nbre d epages ayant au moins une erreur on cherche

E(Y)
soit X le nbre d'erreurs {X=k} pour k décrivant N est un sce

la formule de l 'espérance conditionnelle donne
E(Y) = sigma E (Y l X=k) P(X=k)

puis pour chaque page i= 1,...,n Yi = 1 si au moins une erreur 0 sinon

Yl X = k = sigma sur i Yi l X= k

E(Yi l X=k) = 1- (1-1/n) ^k

on trouve

E(X) = n (1 - exp (-a/n)) et le résultat donné par nuage avec son interprétation judicieuse

[serge75]

sexapil, j'ai un doute sur la compréhension de ton énoncé : ta loi de poisson concerne le nombre d'erreurs par pages (auquel cas cé la réponse de nuage qui est juste) ou le nombre total d'erreurs commises par le scribe (auquel cas c'est la mienne). Ceci dit, après réflexion, la version nuage me parait plus plausible.

[fahr451]

non c'est clair

le nombre total d erreurs est une loi de poisson

et nuage a astucieusement déduit qu'on pouvait considérer que le nbre d'erreurs par page était aussi une loi de poisson

ma preuve n'utilise pas ceci mais est du coup plus longue

[serge75]

Oups, je viens de comprendre où je foirais, et j'avais mal lu l'énoncé (je traitais l'espérance du nombre d'erreurs et non du nombre de pages erronées) ! Au temps pour moi, nuage et fahr vous avez raison !

[jikims31]

bonjour j'ai un probléme je suis en classe de 3éme é je préfére madressé a vous car vous trouveré surmen sur une classe de 30 éléves quelle é la probabilité davoir 2 anniversaire le méme jour? merci de répondre parse ke je suis en galére merci bokou

[kodokan]

Salut,
chaque élève a 1/365 chance de fêter son anniv.
donc on a 30/365 chance qu'un élève A le fête dans la classe
comme il reste 29 élèves dans la classe,
on a 29/360 chance qu'un deuxième élève B fête son anniv.;
la conjonction des deux événements ("anniv. de A" ET "anniv. de B") se traduisant par *, la probabilité recherchée est :
(30/365)*(29/365) (il faut toujours vérifier que le résultat est compris entre 0 et 1 )
J'espère que ce n'est pas faux !

[fahr451]

bonjour

il aurait été nécessaire de créer un nouveau post ...

ce n 'est pas la réponse

la réponse est (au moins deux anniversaire un même jour) 1 - 365x364....X336/(365x365X...x365) il y a 30 nombres dans chaque produit

[nuage]

Salut,

bonjour

il aurait été nécessaire de créer un nouveau post ...

ce n 'est pas la réponse

la réponse est (au moins deux anniversaire un même jour) 1 - 365x364....X336/(365x365X...x365) il y a 30 nombres dans chaque produit

je suis bien d'accord et, comme je suis bon, j'ai fait le calcul.
On trouve


Soit environ 0,7

[gilmat]

Cher Ami
Sur 30 personnes réunies dans une salle la proba que 2 aient leur anniversaire le même jour est 0.706. Autrement dit sur 100 classes de 30 on en aura environ 70 qui auront 2 élèves nés le même jour. C'est un pb simple de proba mais si tes connaissnces en math sont du niveau de celles en ortho tu ne dois pas être capable de comprendre. Je ne suis pas un fana de l'ortho mais quand même il faut respecter son lecteur !
Cordialement
Gilmat