Théorème de Fine-Wilf

[jadis]

Bonjour.
Dans un exercice qui a pour but de démontrer le théorème de Fine et Wilf, on me demande de montrer que si U est un mot de longueur a+b-1 qui est à la fois a-périodique et b-périodique (et que a et b sont premiers entre eux), on a:
où pour ,on définit comme le représentant de tel que .

Je ne sais pas si ça peut m'aider mais j'ai déjà constater que et également que "a barre" et "b barre" sont générateurs de Z/(a+b)Z.

J'ai oublié de préciser que dans la question précédente, j'ai prouvé que la suite d'éléments de Z/(a+b)Z prend une fois et une seule fois chaque valeur non nulle.



Merci d'avance pour votre d'aide.

[jadis]

Je me suis mal exprimé?

[Blueberry]

Bonjour,

dans ton énoncé, ce ne serait pas plutôt un représentant de tel que ?

[jadis]

non c'est bien mod a+b... mais dans l'inégalité je me suis effectivement trompé, c'est ia... et non i.
Je corrige tout de suite

[jadis]

Etant donné que ça n'a pas l'air d'emballer grand monde, je vais reprendre l'exercice depuis le début.

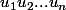
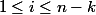
Un mot U de longueur n est une suite de lettres. On dit qu'il est k-périodique si pour tout i tel que on a .

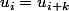
a)Montrer que si un mot de longueur 4 est à la fois 2-périodique et 3-périodique, il est constant, cad que toutes ses lettres sont égales.

Le mot est 2-périodique donc .
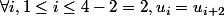
donc 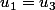et .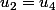
Le mot est 3-périodique donc .
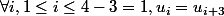
donc .

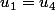
Donc .

Donc le mot est constant.

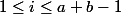
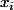
b)Soient a et b deux entiers premiers entre eux. Montrer que la suite d'éléments de prend une fois et une seule chaque valeur non nulle. Pour ,on définit comme le représentant de tel que .

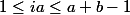
Montrons tout d'abord que a et a+b sont premiers entre eux:

Soit d=pgcd(a,a+b)
On a: d|a et d|(a+b) donc
On prend m=-1 et n=1
On a d|((a+b)-a)
cad d|b.
d|a et d|b donc d|pgcd(a,b)=1
donc a et a+b sont premiers entre eux.

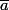
On en déduit directement que est générateur du groupe cyclique .

Démonstration de la question posée:

La suite est une suite d'éléments de et possède exactement a+b-1 éléments.

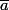
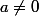
Comme est générateur de , possède tous les éléments non nuls de (puisque a et b sont premiers entre eux donc , et on a ).

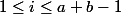
Pour résumer, la suite possède exactement a+b-1 éléments et possède chaque éléments compris entre 1 et a+b-1 (inclus) donc cette suite prend bien une fois et une seule chaque valeur non nulle de .

c) Montrer que si U est un mot de longueur a+b-1 qui est à la fois a-périodique et b-périodique, on a .
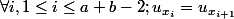
En déduire que U est constant.

Première partie:

JE BLOQUE.... :marteau:

Deuxième partie:

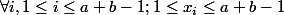
On déduit de la question précédente que donc .
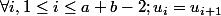
Toutes les lettres sont égales donc U est constant.

d)Démontrer le théorème de Fine et Wilf: Soient a et b deux entiers naturels, et d leur pgcd. Si U est un mot a-périodique et b-périodique de longueur au moins a+b-d, alors u est d-périodique.

Prenons une lettre toutes les d lettres dans U (une lettre sur d). On a alors d mots de longueur a/d +b/d -1 constants d'après la question précédente, ce qui signifie que U est d-périodique puisqu'on a pris une lettre sur d.

[Ted]

J'ai ma petite idée mais je ne sais pas si ça colle avec la suite.
Le probleme est de bien comprendre la signification de uxi je crois.

Si j'ai bien compris, comme il y a une bijection entre les ia et leurs classes non nulles xi, on peut les voir comme égaux.
Alors j'écrirais xi=ia,
donc uxi=uia
et ux(i+1)=u(i+1)a=u(ia+a)
Comme les u sont a periodiques uia=u(ia+a) et le tour est joué.
Je pense que c'est comme ça qu'il faut voir les choses. Après ça rend peut etre la suite plus compliquée mais je n'ai fait qu'y jeter un oeil.

[jadis]

Merci Ted!
Je vais essayer de reprendre ton idée qui a l'air excellente!

Maintenant, il ne reste plus qu'à voir si cette égalité à un sens...

[Ted]

J'espere que personne n'a vu ma remarque précédente qui était fausse.
J'avais en fait presque la reponse mais faute de temps je n'ai pas le temps de corriger completement.
Voila l'idée principale je pense:
en fait entre uxi et ux(i+1) il y a un certain nombre d'elements, mais ce nombre est toujours un multiple de a et (c'est la l'astuce..) ceci est vrai que uxi soit placé avant ou apres ux(i+1) dans le mot!

comme il sont separé d'un multiple de a ils sont egaux par la periodicité.
Pour la suite, comme les uxi parcourent toutes les lettres le resultat est immediat comme tu l'a vu.
Pour le theoreme je n'ai pas regarder
Si l'explication ne suffit pas j'y revinedrait peut etre d'ici la fin du week end s'il le faut.

[jadis]

Oula... Ca se complique.
J'ai bien compris la deuxième partie, du fait de la bijection.
Mais je ne vois pas pourquoi il y a un nombre d'éléments multiple de a entre et ...
Prenons le cas où , on "sort du mot", non?
Ou alors il y a un truc que je ne comprends pas...

[Ted]

ouai en voulant aller trop vite j'ai surement dit une autre betise. Pour etre sur j'vais tout faire a la main:
d'abord faut bien comprendre que la classe de ai, que je noterai [ia] est un ensemble; et xi ,un de ses representants est lui un element de cet ensemble.
alors on écrit:

xi appartient à [ia]={ ia+k(a+b) pour tout k dans z}
de meme
xi+1 appartient à [(i+1)a]={(i+1)a + k'(b+a) k' dans z}

Grace a la question precedente on sait que xi est unique.
Autrement dit il existe un unique ki (car il dépend quand meme de la valeur de i) tel que xi=ia +ki(b+a). Meme chose pour Ki+1 unique pour xi+1.

Or on sait que xi est un indice entre 1 et b+a-1, donc en reprenant l'ecriture precedente

1<= ia +ki(b+a) <= b+a-1
ce qui donne apres bricolage:

(1-ia)/(b+a) <= ki <= (b+a-ia-1)/(b+a)

de meme

(1-a(i+1))/(a+b) <= ki+1 <= (b-ai-1)/(a+b)

en soustrayant,

-1< (-b)/(b+a) <= ki - ki+1 <= 1 +(a-2)/(b+a) <2

donc la difference ki-ki+1 est un entier entre -1 et 2 exclus... Pas trop le choix si ce n'est 0 et 1.

Maintenant si on fait la difference entre xi et xi+1,

xi-xi+1= (a+b) (ki-ki+1) -a

Voyons ce que donne les 2 cas:

si ki-ki+1=0, la difference entre les indices xi et xi+1 est de -a et par periodicité sur a uxi=uxi+1

si ki-ki+1=0, la difference vaut b (xi+1 est alors avant xi dans le mot...) et par la periodicité sur b uxi=uxi+1

Par ailleurs en y regardant de plus pres ta justification de la deuxieme partie est pas tres claire.
Il faut bien remarquer que les indices xi ne sont pas rangés dans un ordre précis, on ne peut donc pas ecrire xi=i ou xi=ai.
On remarque juste que si uxi=uxi+1 pour tout i alors tout les uxi sont égaux comme les xi parcourent tout les indices de 1 à b+a-1 (grace à la bijection) on peut conclure rigoureusement que tout les ui sont égaux

[jadis]

Merci Ted, j'ai bien compris ta méthode.
Mais j'avoue que je n'y aurai jamais pensé...