Intégrales et sommes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 05 Avr 2007, 12:51
par nxthunder » 05 Avr 2007, 12:51
Bonjour a tous,

, On note

=
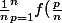)
En utilisant le fait que f sur ] 0 ; 1 ] est strict. décroissante démontrer que, pour p entier naturel vérifiant

on a :
 \le \Bigint_{\frac{p}{n}}^{\frac{p+1}{n}} f(x) dx \le \frac{1}{n} f(\frac{p}{n}))
DOnc ca j'ai réussi ^^
Ensuite en déduire que
 \le \Bigint_{\frac{1}{n}}^{1} f(x) dx \le S_n)
Cest la que je bloque :S
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 05 Avr 2007, 13:43
par nxthunder » 05 Avr 2007, 13:43
UP SVP !!!! :mur:
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 06 Avr 2007, 09:55
par nxthunder » 06 Avr 2007, 09:55
personnes ? :cry: :help:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Avr 2007, 10:01
par tize » 06 Avr 2007, 10:01
nxthunder a écrit:...
En utilisant le fait que f sur ] 0 ; 1 ] est strict. décroissante démontrer que, pour p entier naturel vérifiant

on a :
 \le \frac{1}{n} \Bigsum_{p=1}^n f(\frac{p}{n}) \le \frac{1}{n} f(\frac{p}{n}))
Es-tu sur de ce que tu as écris ? J'ai du mal à croire ceci :
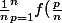 \le \frac{1}{n} f(\frac{p}{n}))
car dans le membre de gauche, si l'on développe la somme il y a déjà
)
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 06 Avr 2007, 10:07
par nxthunder » 06 Avr 2007, 10:07
NoP escuse moi je me suis trompé, j'ai corrigé pardon :S
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Avr 2007, 10:09
par tize » 06 Avr 2007, 10:09
Et bien dans chacun des trois membres des inégalités tu sommes pour p variant de 1 à n et tu retombes sur tes pattes (penses à utiliser Chasles...)
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 06 Avr 2007, 10:56
par nxthunder » 06 Avr 2007, 10:56
tize a écrit:Et bien dans chacun des trois membres des inégalités tu sommes pour p variant de 1 à n et tu retombes sur tes pattes (penses à utiliser Chasles...)
Ah ouaiiiiiiiii je vois comment il faut faire !!!!! Merci infiniment.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités