A propos d'une dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 16:36
par Ivanovich » 28 Mar 2007, 16:36
Bonjour à tous, voila j'ai un probleme pour deriver une fonction pas trop évidente :
=(\frac{20}{x})^4(1-\frac{20}{x})^46)
(c'est une puissance 46)
Il faut utiliser la formule de derivation d'une fonction à la puissance n et de derivation d'une fonction inverse seulement je suis pas sur de mon resultat, si quelqu'un pourrait detailler les étapes ^^
Merci
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 16:42
par fonfon » 28 Mar 2007, 16:42
salut, dis-nous ce que tu trouves tu as peut-être bon
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 16:51
par Ivanovich » 28 Mar 2007, 16:51
=4\frac{-20}{x^2}(\frac{20}{x})^3(1-\frac{20}{x})^46+45\frac{20}{x^2}(1 - \frac{20}{x})^45)
C'est ma premiere ligne de calcul mais j'en suis deja pas sur du tout, ensuite il faudra probablement la factoriser de toute facon ^^
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 17:00
par fonfon » 28 Mar 2007, 17:00
Ivanovich a écrit:=4\frac{-20}{x^2}(\frac{20}{x})^3(1-\frac{20}{x})^46+45\frac{20}{x^2}(1 - \frac{20}{x})^45)
C'est ma premiere ligne de calcul mais j'en suis deja pas sur du tout, ensuite il faudra probablement la factoriser de toute facon ^^
presque
c'est
=4\frac{-20}{x^2}(\frac{20}{x})^3(1-\frac{20}{x})^{46}+(\frac{20}{x})^4\times46\frac{20}{x^2}(1 - \frac{20}{x})^{45})
mets des accolades pour les exposants > à1 chiffre ^{46}
donc c'est un bon début essaie de poursuivre et fais signe
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 17:02
par Ivanovich » 28 Mar 2007, 17:02
ok je savais pas pour l'accolade merci de l'astuce ... erf le 45 c'est une faute de frappe j'ai pas fait attention, bah merci je continue pour voir et j vous dis ^^
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 17:47
par Ivanovich » 28 Mar 2007, 17:47
oula jme perds la j'y arrive pas ... je sais à quoi il faut y arriver mais je comprends pas comment, enfin voila le resultat final apres facto, si quelqu'un peut apporter le détail ... ^^
=2\frac{20}{x^2}(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2+\frac{25\times20}{x}))
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 17:50
par fonfon » 28 Mar 2007, 17:50
=2\frac{20}{x^2}(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2+\frac{25\times20}{x}))
c'est ton prof qui t'a donné ce resultat c'est juste pour savoir la façon pour factoriser car moi je trouve un resultat un peu plus simple
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 17:56
par Ivanovich » 28 Mar 2007, 17:56
j'ai pas compris comment il est arrivé a ce resultat enfin bon tu peux me montrer ce que tu trouves au final stp ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 18:04
par fonfon » 28 Mar 2007, 18:04
il vaut peut-être que j'essaie de retrouver le resultat de ton prof non?
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 18:06
par Ivanovich » 28 Mar 2007, 18:06
ce serait l'ideal ^^
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 18:31
par fonfon » 28 Mar 2007, 18:31
alors
(\frac{20}{x})^3(1-\frac{20}{x})^{46}+(\frac{20}{x})^4(46)(\frac{20}{x^2})(1-\frac{20}{x})^{45})
j'ai mis des parentheses pour que ça soit plus clair donc
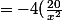(\frac{20}{x})^3(1-\frac{20}{x})(1-\frac{20}{x})^{45}+(\frac{20}{x})(\frac{20}{x})^3(46)(\frac{20}{x^2})(1-\frac{20}{x})^{45})
donc ici j'ai sorti le signe - de -20/x^2 et j'ai transformé un peu donc maintenant on factorise par
(\frac{20}{x})^3(1-\frac{20}{x})^{45})
donc
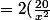(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2(1-\frac{20}{x})+(\frac{20}{x})(23)))
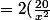(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2+\frac{2\times20}{x}+\frac{20\times23}{x}))
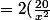(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2+\frac{20(2+23)}{x}))
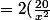(\frac{20}{x})^3(1-\frac{20}{x})^{45}(-2+\frac{20\times25}{x}))
voilà
-
Ivanovich
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Fév 2006, 15:54
-
 par Ivanovich » 28 Mar 2007, 18:46
par Ivanovich » 28 Mar 2007, 18:46
Merci l'ami c'est parfait.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Mar 2007, 18:46
par fonfon » 28 Mar 2007, 18:46
Y-a pas de quoi :++:
A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités