Equation de recurance, convergence.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 22 Mar 2007, 15:14
par Leatherface » 22 Mar 2007, 15:14
Bonjour a tous j'ai un dm a rendre pour mardi prochain et il y a un exercice qui me pose probleme.
Le voici.

Pour la premiere question pas la peine j'ai a peu pres compris.
Mais pour le reste j'aimerais de l'aide car j'ai du mal a comprendre ,
Pour l'equation par recurrence j'en avait deja fait mais la question n'était pas tourné pareil et la je bloque.
Merci d'avance.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Mar 2007, 16:06
par Joker62 » 22 Mar 2007, 16:06
exprime p_t en fonction de p_(t-1) c'est une relation de récurrence.
Pour celà tu fais comme c'est marqué, tu égales les deux membres...
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 22 Mar 2007, 20:48
par Leatherface » 22 Mar 2007, 20:48
Ce qui voudrait dire que normalement:
4p_(t-1) + 6p_t= 30
Mais apres je sais pas si on peut encorereduire l'equation car je sais pas trop si on peut calculer pt et p(t-1) entre eux
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Mar 2007, 21:04
par Joker62 » 22 Mar 2007, 21:04
p_t = 15 - 2*p_(t-1)
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 22 Mar 2007, 21:38
par Leatherface » 22 Mar 2007, 21:38
Je te remercie :++:
Je vais essayer de faire le reste demain.
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 23 Mar 2007, 21:02
par Leatherface » 23 Mar 2007, 21:02
Comment pouvons nous trouver une limite si ils ne precisent pas vers quel valeur Pt doit tendre :hum:

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 23 Mar 2007, 21:34
par nuage » 23 Mar 2007, 21:34
Salut,
on a

.
Si il y a une limite

elle est solution de l'équation

.
Cette équation est facile à résoudre et donne un candidat pour la limite.
La question suivante permet de prouver la convergence de la suite des prix vers cette limite.
-
Anonyme
 par Anonyme » 24 Mar 2007, 17:17
par Anonyme » 24 Mar 2007, 17:17
mais comment etudier la convergence de cette fonction. je ne sais pas comment m'y prendre?,???

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 24 Mar 2007, 19:40
par nuage » 24 Mar 2007, 19:40
Salut,
je pense que tu as trouvé
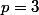
.
On a donc

.
On reporte ceci dans l'égalité

et on obtient
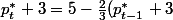)
d'où

.
On pense alors aux suites géométriques.
A+
-
Anonyme
 par Anonyme » 25 Mar 2007, 13:34
par Anonyme » 25 Mar 2007, 13:34
bon d'accord mais ca je l'ai deja trouvé.mais après comment il faut faire pour prouver que cette suite est convergente. merci
-
mathelot
 par mathelot » 25 Mar 2007, 14:21
par mathelot » 25 Mar 2007, 14:21
11235 a écrit:mais comment etudier la convergence de cette fonction. je ne sais pas comment m'y prendre?,???
il y a toute la classe qui rapplique :zen:
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 25 Mar 2007, 17:39
par Leatherface » 25 Mar 2007, 17:39
Toute la Fac plutot :zen:
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 26 Mar 2007, 11:21
par Leatherface » 26 Mar 2007, 11:21
nuage a écrit:Salut,
on a

.
Si il y a une limite

elle est solution de l'équation

.
Cette équation est facile à résoudre et donne un candidat pour la limite.
La question suivante permet de prouver la convergence de la suite des prix vers cette limite.
Enfaite Nuagej suis ok pour pt= 5 - 2/3pt-1
Mais apres je sais pas comment tu es passé a

:hum:
Merci

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 26 Mar 2007, 11:27
par nuage » 26 Mar 2007, 11:27
on a une suite définie par
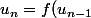)
.
Si elle a une limite finie

celle ci vérifie
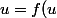)
.
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 26 Mar 2007, 19:53
par Leatherface » 26 Mar 2007, 19:53
Merci beaucoup Nuage et aux autres qui m'ont aidé.
Sinon il reste encore une petite question dans mon dm .
C'est une limite qui m'embete.
g(x) = racinex-racine3/ x-3
Il faut trouver sa limite lorsque x tend vers 3

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 26 Mar 2007, 21:25
par nuage » 26 Mar 2007, 21:25
Salut,
^2-(\sqrt3)^2}= \frac1{\sqrt{x}+\sqrt3})
si x>0
-
Leatherface
- Messages: 9
- Enregistré le: 07 Mar 2007, 11:38
-
 par Leatherface » 26 Mar 2007, 21:37
par Leatherface » 26 Mar 2007, 21:37
Super sympa de ta part nuage
Merci encore une fois :+:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités

