DM Analyse elementaire, suites.

[Ben86000]

Bonjour à vous,
Je suis en L1 en fac de sciences de Poitiers, et je n'arrive pas à terminer un DM sur lequel je bosse depuis 2 semaines. Voila les 2 questions qui me posent probleme :


On considère ici un nombre réel irrationel positif x, ainsi qu'une suite (Xn) de nombres rationnels strictement positifs qui converge vers x.
Pour tout n, on note Pn et Qn les entiers positifs tels que la fraction réduite donnant Xn soit Xn= Pn/Qn.

1. On suppose que (Qn) ne tend pas vers +oo. Montrer qu'il existe une sous-suite de Xn qui est constante et aboutir à une contradiction.

2. En déduire que (Pn) et (Qn) tendent toutes deux vers +oo.


J'attends votre aide avec impatience, merci beaucoup par avance.

[Blueberry]

Bonjour,

Dire que Qn ne tend pas vers +inf signifie que :

Il existe A tq, qq soit N entier il existe n >= N tel que Qn <= A.

Cela permet de construire une suite extraite de (Qn) notée (Qnk) (k = 0,1,...) qui vérifie : pour tout k, 0 < Qnk <= A .Mais alors cette suite Qnk ne prendrait q'un nombre fini de valeurs et l'une de ces valeurs serait prise une infinité de fois par la suite (Qnk). et donc par la suite (Qn)

Ceci permet d'extraire de (Qn) une suite constante.

[mathelot]

Soit
une suite de limite .

la suite étant convergente dans est une suite de Cauchy.

Faisons l'hypothèse absurde que ne tende pas vers

il existe un entier g tel que est majorée par



Ecrivons le critère de Cauchy:





pour assez petit inférieur à ,

l'entier est nul.

La suite est donc constante à partir du rang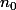

Comme cette suite est constante, elle tend vers elle-même et
x est rationnel. Nous obtenons une contradiction. La suite n'est pas majorée.

Ecrivons:

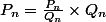
En passant à la limite,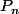 tend vers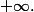
car le quotient tend vers .



Cordialement,

[Ben86000]

Merci pour vos réponses mais je ne comprends pas quelque chose :

Pourquoi est-ce que :
Pour epsilon inferieur a 10^-2g, l'entier PpQn-QpPn est nul et non inférieur à 1. Et pourquoi peux t'on alors dire que Xn est constante ?

Merci encore pour votre aide.

[mathelot]

que vaut un entier naturel très petit ? disons inférieur à

Par ailleurs,

assez grands,



par la transitivité de l'égalité, il y a une valeur commune, constante ...

[Ben86000]

Ok, bien compris.
Merci encore pour ton aide.
A bientot.