Gradiant

[rifly01]

Bonjour,


J'ai une question brêve : Que vaut dire gradiant .. (au dela de la définition formelle), que signifie t-il concrètement ...


Merci

[jose_latino]

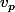Il serait intéressant savoir qu'est-ce que tu étudies et ton niveau d'études. Sinon on pourrait dire des choses qui ne te servent pas à rien. Je te donne la définition pour les gens qui font des mathématiques: Si une application ( ouvert de ) est différentiable en , donc le gradient de en est l'unique vecteur tel que: , pour tout , normalement, on note ou à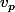

[jose_latino]

L'interprétation du gradient est qu'il sagit de la direction où la fonction change plus rapidement. Si la fonction est la temperature, le gradient t'indique dans quelle direction tu dois te déplacer à partir de un point pour sentir la variation plus rapide de la temperature.

[Dominique Lefebvre]

L'interprétation du gradient est qu'il sagit de la direction où la fonction change plus rapidement. Si la fonction est la temperature, le gradient t'indique dans quelle direction tu dois te déplacer à partir de un point pour sentir la variation plus rapide de la temperature.

Bonjour,

Plus précisément, on démontre facilement que le vecteur grad f est normal aux surfaces de niveau f = cte et qu'il est dirigé vers les valeurs croissantes de f.