pouvez m'aider à résoudre ces deux équations:
x²-3x-3 <= 0
et
x²-x-3 >= 0
Merci d'avance pour votre aide
Aide sur résolution équation
9 messages
- Page 1 sur 1
Bonjour
1)x² - 3x - 3<=0
delta = 9 + 12 = 21
x=( 3-v21)/2 et (3+v21)/2
x...................(3-v21)/2.............(3+v21)2.......
e+++++++++++++0-----------------.+++++++
S = [(3-v21)/2;(3+v21)/2]
2)x² - x - 3 > = 0
delta = 1+12 = 13
x=( 1-v13)/2 et (1-v13)/2
x.....................(1-v13)/2...........(1+v13)/2........
E++++++++++++++++0---------------0+++++++
S = ]-oo;(1-v13)/2]U[(1+v13)/2;+oo[ :id:
1)x² - 3x - 3<=0
delta = 9 + 12 = 21
x=( 3-v21)/2 et (3+v21)/2
x...................(3-v21)/2.............(3+v21)2.......
e+++++++++++++0-----------------.+++++++
S = [(3-v21)/2;(3+v21)/2]
2)x² - x - 3 > = 0
delta = 1+12 = 13
x=( 1-v13)/2 et (1-v13)/2
x.....................(1-v13)/2...........(1+v13)/2........
E++++++++++++++++0---------------0+++++++
S = ]-oo;(1-v13)/2]U[(1+v13)/2;+oo[ :id:
Bon : je suis nouveau sur ce forum, et je dois admettre qu'il y a un truc qui me saoule énormément : c'est l'illisibilité de certains posts.
Je suggère a ceux qui demande des réponse sur ce site qu'ils apprennent les bases de , ca simplifierais la vie de beaucoup de membres!
, ca simplifierais la vie de beaucoup de membres!
Voici un site donnant les bases de :
:
http://www.les-mathematiques.net/p/p/l/
Alphonse $BigCap$ Capriani
Je suggère a ceux qui demande des réponse sur ce site qu'ils apprennent les bases de
Voici un site donnant les bases de
http://www.les-mathematiques.net/p/p/l/
Alphonse $BigCap$ Capriani
Première inéquation : 
Soit défine par
défine par  = x^2-3x-3)
On veut donc étudier le signe de f!
On résoud d'abord l'équation=0) :
:
Le discriminant de est
est 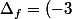^2-4\times(-3) = 21)
 , donc l'équation
, donc l'équation =0) possède deux racines réelles distinctes que l'on note
possède deux racines réelles distinctes que l'on note  .
.
On a :
[center] [/center]
[/center]
Concernant le signe de , on regarde le signe de son coefficient dominant (coefficient du monôme de plus haut degré)
, on regarde le signe de son coefficient dominant (coefficient du monôme de plus haut degré)
Ici le coefficient dominant est égal à 1 donc est positif.
Donc est positive strictement sur
est positive strictement sur  , nulle sur
, nulle sur  et strictement négative sur
et strictement négative sur 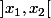
D'ou le tableau de signe de :
:
[center]
 & & + & 0 & - & 0 & + & \\ \hline<br />\end{tabular})
[/center]
Et donc la solution de l'inéquation \leq 0) est l'intervalle
est l'intervalle 
La deuxième inéquation se résoud exactement de la même manière!
____________________________________________________
PS : Je ne m'appelle pas Kaspita, mais Alphonse $BigCap$ Capriani!!!
Soit
On veut donc étudier le signe de f!
On résoud d'abord l'équation
Le discriminant de
On a :
[center]
Concernant le signe de
Ici le coefficient dominant est égal à 1 donc est positif.
Donc
D'ou le tableau de signe de
[center]
[/center]
Et donc la solution de l'inéquation
La deuxième inéquation se résoud exactement de la même manière!
____________________________________________________
PS : Je ne m'appelle pas Kaspita, mais Alphonse $BigCap$ Capriani!!!
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 116 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
