égalité remarquable avec normes ?

par **totor** » 12 Mar 2007, 12:26

Bonjour,

j'aimerai savoir si les égalités remarquables marchent avec les normes, par exemple est ce que l'on a :

merci par avance

par **titine** » 12 Mar 2007, 13:17

Il faut savoir de quoi on parle.
Je pense que tu parles de la norme de vecteur telle qu'on la définit au lycée.
Soit a et b des vecteurs.
lla-bll désigne la norme du vecteur a-b.
Mais que désigne llabll. Le seul produit de vecteurs étudié au lycée est le produit scalaire. Or le produit scalaire de 2 vecteurs est un nombre. Norme d'un nombre ??

Ce qui est exact,c'est :
llvec(a)-vec(b)ll² = llvec(a)ll² + llvec(b)ll² - 2 vec(a).vec(b)
Où vec(a).vec(b) représente le produit scalaire des 2 vecteurs.

par **totor** » 12 Mar 2007, 13:35

titine a écrit:Il faut savoir de quoi on parle.
Je pense que tu parles de la norme de vecteur telle qu'on la définit au lycée.
Soit a et b des vecteurs.
lla-bll désigne la norme du vecteur a-b.
Mais que désigne llabll. Le seul produit de vecteurs étudié au lycée est le produit scalaire. Or le produit scalaire de 2 vecteurs est un nombre. Norme d'un nombre ??

Ce qui est exact,c'est :
llvec(a)-vec(b)ll² = llvec(a)ll² + llvec(b)ll² - 2 vec(a).vec(b)
Où vec(a).vec(b) représente le produit scalaire des 2 vecteurs.

salut,
Merci pour ta réponse. Est ce que

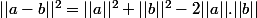
serait équivalent à ta définition ?

merci encore

par **titine** » 12 Mar 2007, 13:54

Non ! Sauf dans le cas où a et b sont des vecteurs colinéaires. En effet :
vec(a).vec(b) = llall * llbll * cos(a,b)

par **totor** » 12 Mar 2007, 14:07

titine a écrit:Non ! Sauf dans le cas où a et b sont des vecteurs colinéaires. En effet :
vec(a).vec(b) = llall * llbll * cos(a,b)

D'accord ! merci

Mais comment arrive t-on sur ton résultat ? Est ce dur à démontrer ?

merci

par **titine** » 12 Mar 2007, 17:24

Cherche un cours sur le produit scalaire niveau 1S.
Tu dois trouver ça sur Internet (Wikipédia, ....)

égalité remarquable avec normes ?

égalité remarquable avec normes ?

Qui est en ligne