Limite en 0 d'une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
darkomen
- Membre Naturel
- Messages: 89
- Enregistré le: 07 Aoû 2006, 12:00
-
 par darkomen » 11 Mar 2007, 18:17
par darkomen » 11 Mar 2007, 18:17
Salut à tous,
Voilà je pense que mon problème n'est pas très compliqué mais je n'arrive pas à comprendre.Je vous fait part de l'enoncé et du corrigé en ésperant que vous puissiez répondre à ma question.
---------------------------------------------------------------------------
Determiner, lorsqu'elle existe, la limite en 0 de chacune des fonctions suivantes:
2/=\frac{x^2-5x}{x})
Le corrigé me dit que n'est pas définie en 0, mais pour tout
n'est pas définie en 0, mais pour tout 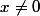 ,
,=x-5)
---------------------------------------------------------------------------
Comment la correction arrive au résultat de=x-5) je ne comprend pas?
je ne comprend pas?
pourriez vous me détaillés la démarche mathématique pour trouver cela?Merci de votre precieuse

-
susan_mayer
- Membre Relatif
- Messages: 179
- Enregistré le: 24 Sep 2006, 16:48
-
 par susan_mayer » 11 Mar 2007, 18:23
par susan_mayer » 11 Mar 2007, 18:23
parce que si x=0 on a f(0)=(0²-5*0)/0
et cela nexiste pas
et puis si tu simplifie f tu as :
(x²-5x)/x
tu factorise par x:x(x-5)/x
tu as donc:
f(x)=x-5
-
darkomen
- Membre Naturel
- Messages: 89
- Enregistré le: 07 Aoû 2006, 12:00
-
 par darkomen » 11 Mar 2007, 18:49
par darkomen » 11 Mar 2007, 18:49
A oui en factorisant que je suis bete..EVIDEMENT tous s'explique.
J'etais un desesperate houseman et tu ma sauvé merci Susan mayer
Merci antonin aussi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
