Equicontinuité

[bibup]

Bonjour,
Il faut que je montre si les familles suivantes sont equicontinue et/ou uniformement equicontinue:
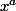
a) { : a>0} avec x>=0
b) {sin(rx) : r dans R}
c) {sin(+r : r dans R}

On a montré l'equicontinuité du c) et la non equicontinuité de a) et b). Mais je ne comprends pas trop ce qu'on a fait. et pour uniformément continue, je n'arrive pas à commencer, à trouver le contre-exemple si ca ne l'ai pas ou comment partir si c'est uniformement equicontinue.
Merci

[fahr451]

bonjour

pour moi équicontinue contient dans la définitionl' uniformité par rapport à la
variable donc je ne sais pas ce que signifie uniformément équicontinue

redonne donc "tes" définitions de ces notions

[bibup]

equicontinuité :
soit E un espace metrique.
(fn) une suite de fonction sur E et x un point de E.
On dit que la suite est equicontinue si:

[fahr451]

entendu

pour moi équicontinuité c'était ce que tu appelles uniforme équicontinuité

[fahr451]

donc uniforme équicontinuité implique l'uniforme continuité de chaque fonction

est-ce le cas du c) ?

[bibup]

c'est les deux definitions que j'ai dans mon cours.
Mais je suis vraiment perdu avec toutes ces definitions( unif. continue, lipschitzienne, equi-lipschitzienne ...). Je m'embrouille totalement.
Sur les 3, j'ai l'impression que il n'y a que la c) d'uniformement equicontinue, mais je ne sais pas comment les montrer.

[fahr451]

reprenons

uniforme équicontinuité implique équicontinuité non?

comme tu dis que a) et b) ne sont pas équicontinues la question de l'uniforme équicontinuité ne se pose pas

l'uniforme équicontinuité est la continuité uniforme "de la même façon" pour toutes les fcts ; elles doivent donc être déjà toutes uniformément continues

or x-> sin ( x^2) ne l 'est pas

[bibup]

donc pour montrer l'uniforme equicontinuité, il faut passer par la continuité?

[bibup]

sin(x^2) n'est pas uniformement continue car sa dérivée n'est pas bornée, du coup, elle n'est pas uniformement equicontinue.
et par exemple, cette fonction :
{sin(x-r) : r dans R}
Elle est equicontinue car equi-lipschitzienne et elle est uniformement continue car sa dérivée est bornée, donc elle est uniformément continue?

[fahr451]

ex 1
le fait que la dérivée ne soit pas bornée est la raison intuitive pour voir qu 'elle n'est pas uniformément continue mais ne constitue pas une preuve

ex 2
oui si la dérivée est bornée alors le TAF donne lipschitzienne qui implique uniformément continue

[bibup]

Merci bcp,je sais que pour l'exemple 1 je dois trouver un contre-exemple, mais au moins j'ai compris.

[fahr451]

il y a une façon agréable séquentielle de prouver la non uniforme continuité de f

trouver deux suites u et v avec un-vn ->0 et f(un) -f(vn) ne tendant pas vers 0