Polynomes de newton (sup)

par **urza** » 11 Mar 2007, 14:55

Bonjour à tous,
On definit

et

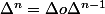
ainsi que la famille de polynomes

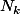
telle que

Trouver

Moi j'ai

mais ça m'a l'air faux ...
Merci de votre aide.

par **fahr451** » 11 Mar 2007, 15:01

bonjour

un petit souci de signe

par **urza** » 11 Mar 2007, 15:07

Ok c'est du

mais pour la suite c'est une composition n fois par Delta ?

par **fahr451** » 11 Mar 2007, 15:15

ben oui tu l'as toi même écrit...

par **urza** » 11 Mar 2007, 15:24

D'accord mais apres je trouve

et ca va pas pour tout n et tout k natuels...

par **fahr451** » 11 Mar 2007, 15:36

en effet
delta N0 = ?

par **urza** » 11 Mar 2007, 15:40

par **urza** » 11 Mar 2007, 15:44

Si n>k ca pose pb non ?

par **fahr451** » 11 Mar 2007, 15:44

en effet ce qui a des conséquences sur delta^n deNk