Aide exercice fonction 1ere S

[riquelme1990]

Soit f la fonction déninie sur R/(2) par:f(x)= (ax²+bx+c)/(x-2) et (C) sa courbe représentative dans un plan muni d´un repére orthonormal. Déterminez a,b,c pour que (C) ait les propriété suivantes:

-(C) passe par le point A(0;5)
-la tangente a (C) au point A est parallele a laxe des abscisses
-la tangente a (C) au point B d´abscisse 1 a pour coefficient directeur -3

je ne sais pas comment faire

[titine]

-(C) passe par le point A(0;5)
Qu'est ce que ça signifie pour la fonction f ?

-la tangente a (C) au point A est parallele a laxe des abscisses
Que peut on en déduire ?

-la tangente a (C) au point B d´abscisse 1 a pour coefficient directeur -3
Et là ?

[maf]

Hello, premièrement, le point A doit vérifier la courbe donc :

f(0) = 5 d'où donc tu as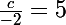

un petit rappel pour le reste ... la pente de la tangente est la dérivée ! :id:

[titine]

maf laisse le temps à riquelme1990 de chercher et de répondre.
Merci !

[titine]

le point A doit vérifier la courbe

Très mal dit !
Un point ne "vérifie" pas une courbe. Un point appartient à une courbe.

[maf]

vérifier l'équation de la courbe désolé ... le mot m'a échappé

[riquelme1990]

-1ere hypothese = f de 0 =5
- 2eme hypothese = la derivee est nulle donc pas de coefficient directeur pour ce point
- 3eme hypothese f´(1) = -3 donc decroissante

voici les signification que jai trouver,mais quel est le rapport avec a,b et c.comment peut on les trouver?

[maf]

Arrive tu as nous dire comment tu peux trouver f(0) ? en remplaçant x par 0 dans l'équation non ?

Quelle est la dérivée de la fonction ?

En remplaçant tour à tour les données que tu as, tu va trouver toutes les inconnues ... (je t'ai donné, par maladresse, la première solution)

[riquelme1990]

dc on sait que c = -5/2

et que la dérivée de f est égale a (ax²+2bx-2b+c)/((x-2)²)

mais ques qu´on peut faire avec cette derivée? c en trouvant f´(1) de (2) et de (3) et apré en additionant ou soustrayant les réponses qu´on trouvra a et b???

[maf]

Petite correction pour la dérivée ...

dc on sait que c = -5/2

et que la dérivée de f est égale a (ax²+4ax-2b+c)/((x-2)²)

mais ques qu´on peut faire avec cette derivée? c en trouvant f´(1) de (2) et de (3) et apré en additionant ou soustrayant les réponses qu´on trouvra a et b???

[maf]

La pente de la tangente au point A est f'(0), celle-ci doit être parralèle à l'axe des abscisses --> doit avoir la même pente ... :id:

et f'(1) = -3

puisque tu connais déjà c ... tu auras 2 équations, 2 inconnues :id: :id:

[riquelme1990]

nan on a faux jcroi ,c f´(x)= (u´v-v´u)/v²
=((2ax+b)(x-2)-1(ax²+bx +c))/((X-2)²)
=(2ax²-4ac+bx-2b-ax²-bx-c)/((x-2)²)
=(ax²-4ax-2b-c)/((x-2)²)

mais apré pour trouver a et b y faut faire ske g dit avant nan?

[maf]

Ta dérivée est juste cette fois ...

Simplement je sais pas ce que tu entends par f'(1) (2) et (3)

moi je ferais f'(0) et f'(1) mais après je ferais aucune réflexion sur croissant, décroissant ...

pose simplement f'(0) = 0 et f'(1) = -3

[riquelme1990]

oui ok merci titine et maf

ca fera f´(0)=(-2b+5/2)/(0-2)²=0
=-2b/4=-5/2
b=-5/4
et apré on fai pareil avec f´(1) ou on trouvra a
merci beaucoup :ptdr: