Accroissements finis

par **yocto** » 07 Mar 2007, 17:58

Bonjour, en utilisant le théoreme des accroissements finis je dois montrer que

Merci de votre aide

par **yos** » 07 Mar 2007, 18:04

Bonjour.
Sur l'intervalle [1;4/3] sans aucun doute.

par **yocto** » 07 Mar 2007, 18:08

Bah c'est bien ce que j'ai essayé de faire mais vu l'encadrement de la dérivée de arctan(x), j'arrive pas au résultat demandé ...

par **Joker62** » 07 Mar 2007, 18:08

Soit f : [a, b]

R une fonction à valeurs réelles (a et b réels tels que a < b). Si :

* f est continue sur l'intervalle fermé [a, b]
* f est dérivable sur l'intervalle ouvert ]a, b[
* il existe k réel positif tel que, pour tout élément x de ]a, b[, |f'(x)|

k,

alors

Ici on a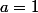

( car

) et

Tu sais qu'il existe

etc... etc...

Edit : oups

par **yocto** » 07 Mar 2007, 18:13

oui en effet merci

J'dois vraiment etre crevé, j'avais gardé 0<=f'(x)<=1 ....

C'est tout bête en fait :we:

Accroissements finis

Accroissements finis

Qui est en ligne