Polynomes et trigo.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 09:27
par Epsilon » 09 Fév 2007, 09:27
bonjour ,
je suis en train de de reviser les cours sur les EDP
et je me bloque sur cette question
soit
=cos(n(arccos(x)))
et

monter que
)
est un polynome (en fonction de x ).
merci
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Fév 2007, 09:31
par fahr451 » 09 Fév 2007, 09:31
bonjour
on pose t = arcos x , cos t = x
T(x) = cos (nt) qui doit s exprimer comme un polynôme en cost
pour cela on utilise
cosnt = RE ( e^(int)) = Re (cost +isint)^n = développer par binôme
T = polynôme de chebychev de première espèce
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 09 Fév 2007, 09:34
par andros06 » 09 Fév 2007, 09:34
Hello ;-)
Tu peux poser thêta=arcos(x) donc pour tout thêta , on a :
Tn(cos(thêta))=cos(n*thêta). Avec un ptit coup de trigo tu devrais t'en sortir
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 09 Fév 2007, 09:35
par andros06 » 09 Fév 2007, 09:35
Aaaaargh. Fahr qui répond plus vite que son ombre ! (et que moi en l'occurence)
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 09:41
par Epsilon » 09 Fév 2007, 09:41
merci fahr
si j'ai bien compris
T(x)=cos(n*t)=Re
^k*(i*sin(t))^{nk}})
am I right?
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 09:51
par Epsilon » 09 Fév 2007, 09:51
mais je vois un polynome en de cos(t)
:triste: :triste: :cry:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Fév 2007, 10:29
par fahr451 » 09 Fév 2007, 10:29
fais porter le n-k sur le cos plutôt
le terme i^k sin^k t est réel ssi i est pair k = 2p
il vaut (-1)^p (sin^2 t)^p = (-1)^p (1-cos^2t)^p : polynôme en cost
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 11:36
par Epsilon » 09 Fév 2007, 11:36
:we: :we: :we:
merci fahr et andros
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 09 Fév 2007, 14:07
par abcd22 » 09 Fév 2007, 14:07
Pour démontrer l´existence des polynômes de Tchebychev (et aussi trouver le degré et le coef dominant mais c´est inutile ici) ça va plus vite en utilisant
x)} + \cos{(nx)} = 2 \cos{x}\, \cos{((n+1)x)})
et une récurrence.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 14:32
par Epsilon » 09 Fév 2007, 14:32
salut abcd
tu ma donné une formule sans démonstration
est elle vérifié ?
perso je la connais pas !
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 09 Fév 2007, 14:50
par abcd22 » 09 Fév 2007, 14:50
C´est un cas particulier de
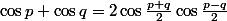
, qui se démontre en écrivant
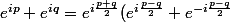 = 2 \cos{\frac{p-q}{2}}e^{i\frac{p+q}{2}})
et en prenant la partie réelle. On a une formule analogue avec les sin en prenant la partie imaginaire, et on trouve une formule pour

par la même méthode.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 09 Fév 2007, 15:01
par Epsilon » 09 Fév 2007, 15:01
:mur: :mur: ah oui c vrai
merci abcd
:we: :we:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Fév 2007, 15:30
par fahr451 » 09 Fév 2007, 15:30
abcd je pense moi que ça va plus vite de donner directement l 'expression polynômiale pas de récurrence à faire; en revanche l 'expression est inutilisable( elle donne degré et coeff dominant cependant) et la relation de récurrence est nécessaire pour pratiquement toutes les questions qui traitent de ces polynomes.
-
Jonathan_
- Membre Naturel
- Messages: 41
- Enregistré le: 16 Déc 2006, 19:37
-
 par Jonathan_ » 03 Mar 2007, 14:38
par Jonathan_ » 03 Mar 2007, 14:38
Est-ce-que vous avez une méthode pour avoir lemême résultat mais avec des cosinux hyperboliques... c'est à dire montrer que quelquesoit aIR, Tn(ch(a))=ch(n*a) ??? parce que j'ai essaye en decomposant avec les exponentielles, mais j'arrive pas a aboutir, je reste toujours coincé...
-
chadiou
- Membre Naturel
- Messages: 26
- Enregistré le: 02 Mar 2007, 16:44
-
 par chadiou » 03 Mar 2007, 14:49
par chadiou » 03 Mar 2007, 14:49
slt vous pouvais m'aider aller voir mon exo sil vous plait
-
Jonathan_
- Membre Naturel
- Messages: 41
- Enregistré le: 16 Déc 2006, 19:37
-
 par Jonathan_ » 04 Mar 2007, 12:37
par Jonathan_ » 04 Mar 2007, 12:37
Petit up... personne ne peut m'aider??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités