Bornes d'un ensemble
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yocto
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Déc 2006, 20:33
-
 par yocto » 27 Fév 2007, 17:29
par yocto » 27 Fév 2007, 17:29
Bonjour à tous.
Je dois déterminer si elles existent les bornes inférieures et bornes supérieures de l'ensemble suivant et dire si elles appartiennent à l'ensemble en question :
^n , n > 0})
(n appartient à N*)
Je trouve sup A=3/2 et qui appartient a A
et inf A=-1 qui n'appartient pas a A
Pouvez vous confirmer si c'est juste et comment je dois le démontrer. Doit on forcément considérer les suites extraites
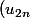)
et
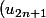)
de
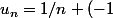^n)
Merci de votre aide.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 27 Fév 2007, 17:56
par fahr451 » 27 Fév 2007, 17:56
bonsoir
ça me semble juste et ça me semble inévitable (même si on peut bricoler avec epsilon sans parler des suites extraites)
-
yocto
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Déc 2006, 20:33
-
 par yocto » 27 Fév 2007, 18:14
par yocto » 27 Fév 2007, 18:14
En fait j'en ai un second plus dur :we:
B={

, n app. à N*}
où E[.] désigne la partie entière.
je trouve sup B = 5/2 qui appartient à B
et inf B = 5/6 qui appartient aussi à B
Je sais pas si c juste et surtout quelqu'un peut m'aider à le démontrer ? merci
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 27 Fév 2007, 18:27
par fahr451 » 27 Fév 2007, 18:27
en notant a(n) les éléments
pour n>= 4 on a (n+4)/n =< 2 donc a(n) =< 2n/(n+1) <2
on regarde a(1),...,a(4) le max est pour a(1) = 5/2 >2
donc le sup est 5/2
pour n>=5 on a n/(n+1) >=5/6 et (n+4)/n >1 donc a(n)>= 5/6
on regarde a(1),...,a(5) le min est pour a(5) = 5/6 donc 5/6 est l 'inf
-
mathelot
 par mathelot » 27 Fév 2007, 18:28
par mathelot » 27 Fév 2007, 18:28
bonsoir,
la suite s'étudie en considérant séparemment les 4 premiers termes (à calculer)
et ensuite:
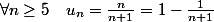
-
yocto
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Déc 2006, 20:33
-
 par yocto » 27 Fév 2007, 18:34
par yocto » 27 Fév 2007, 18:34
ok merci pour votre aide :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
