Barycentre 1ere S

[Muiathai]

tout d'abord bonjour a tous,
Mon probleme et un exercice simple en soi:

Soit un tétraedre ABCD,F le millieu de [AD],G le centre de gravite
du triangle ABC et E le point du plan tel que BDCE soit un parallelogramme.
1)Montrer que D est le barycentre de (B;1),(C;1)et(E;-1)
2)Montrer ques les points E,F,G sont aligne

je l'ai commence mais je suis bloque car je ne sais pas si je dois utilisait le theoreme d'associativite.

merci pour toute reponse

[Muiathai]

s'il vous plait juste une piste parceque je m'embrouille :triste:

merci d'avance pour quiconque me repondrait

[Muiathai]

ainsi c'est bien ce que je pensait de ce forum
dommage :doh:

[Muiathai]

nn serieu j'ai l'impression que tout le monde :dodo:
:help: quoi!
P.S:j'ai deja fait l'exo je veux juste etre sur que c'est bon c un exo de DM

[lexot]

Bonjour

D est le barycentre de (B;1),(C;1)et(E;-1), donc :
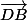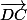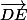+-= démontrable en géométrie de 2nde

D est le barycentre de (B;1),(C;1)et(E;-1), donc :
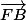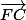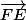+-= (1)

F milieu de A et D, donc F est le barycentre de (A;1), et(D;1), donc :
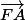+= (2)

G est le centre de gravité du triangle ABC, donc G est le barycentre de (A;1),(B;1)et(C;1)
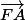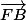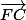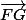++= (3)

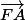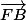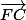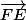(1) et (2) => ++-= (4)

(3) et (4) => -=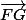
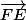Les points E, F, et G sont donc alignés

Cordialement

[Muiathai]

oui merci lexot
par contre pour la 2 j'ai utilisé le theoreme d'associativité!
merci quand meme c'est un DM on sait jamais!

et pour la 1 c'est du fait que ,par exemple, G barycentre de (A,a), (B,b),(C,c) alors on a aGA+bGB+cGC=o

d'ou pour ici DB+DC-DE c'est enfantin

merci lexot tu as participer et eventer quelque soupcons que j'avais :++: