Fonctions primitives

par **Momo_ouioui** » 22 Fév 2007, 18:59

Bonjour,

Comment trouver la fonction primitive F' d'une fonction f? Quelle est la méthode?
Par exemple, comment trouver une primitive de f, sur R, quand f(x)= x²?

Merci

par **Nightmare** » 22 Fév 2007, 19:00

Bonsoir

Il n'y a pas de formules directes à appliquer, lorsqu'on dérive. Il y a des formules qui marchent pour certaines fonctions, mais on ne peut pas trouver les primitives de toutes les fonctions.

Les primitives de la fonction

sont les fonctions

.
On a même la formule :

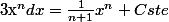
Mais par exemple tu ne pourras pas trouver de primitive de la fonction

:happy3:

par **Charlotte59** » 22 Fév 2007, 19:01

La plupart du temps, on utilise des formules :

pour x^n : la primitive est (x^(n+1)) / (n+1) : (ou (x^(n+1)) / (n+1) + une constante si on veut être précis)

Donc la primitive de x^2 est (x^3) / 3, ms au cas où tu as un doute, il suffit de re-dériver.

par **Momo_ouioui** » 23 Fév 2007, 13:52

Merci beaucoup pour les réponses, mais j'ai une remarque qui peut paraître assez idiote: je ne comprend pas pourquoi l'on doit ajouter une constante à la fonction primitive?

J'ai une autre question: Comment fait-t-on pour déterminer la famille (Pm) ,m appartenant à R, à un paramètre, des primitives de la fonction polynôme p définie sur R par p(x)= x²-x+1?

Merci

par **Nightmare** » 23 Fév 2007, 13:55

Car tu sais que la dérivée d'une constante est nulle, donc si on l'ajoute à une fonction, on obtiendra toujours la même fonction à l'arrivée en dérivant.

Par exemple tu sais que la dérivée de x est 1
Donc une primitive de 1 est x.
Mais tu sais aussi que la dérivée de x+124 est 1, ou encore la dérivée de x-1241894164 est aussi 1.

En fait, toutes les fonctions de la forme x->x+C où C est une constante ont pour dérivée 1, on dit que ces fonctions forment l'ensemblent des primitives de la fonction x->1.

Avec cette explication tu devrais t'en sortir pour l'exercice avec Pm

:happy3:

Fonctions primitives

Fonctions primitives

Qui est en ligne