Dérivées
32 messages
- Page 1 sur 2 - 1, 2
Dérivées
Bonjour les Gens !!! :zen:
Et bien voila jai un autre exercice à faire mais cette fois ci sur les dérivées ...
Voici lénoncé :
Une fonction f définie sur R
f(x) = x(x+1)
x-2
1.étudiez son sens de variations de la fonction f ainsi que les limites aux bornes de son ensemble de définition (interprétez graphiquement ces résultats lorsquils le permettent)
JAI TROUVE pour la dérivé :
f(x) = x² - 4x -2
(x- 2)²
Mais après je bloque et cest quoi lensemble de définition de la dérivée ?
Merci pour votre aide ...
2) a. Montrez qu'il existe trois réels a, b, c tels que , pour tout x appartenant à R , on ait : f(x) = ax + b+ c/x-2
b. Soit delta la droite d'équation y = ax+b , pour les valeurs de a et b trouvées à la question a. Que représente la droite delta pour la courbe C ? ( justifiez)
c. Etudiez la position de C par rapport à la droite delta
d. déterminez le plus petit entier n tel que : si valeur absolu de x supérieur ou égal à n, alors valeur absolu de f(x) - ( ax+b) inférieur ou égal à 10^-1
e. trouvez tous les points de C dont les coordonnées sont des entiers relatif
suite après et oui c'est pas finit
Et bien voila jai un autre exercice à faire mais cette fois ci sur les dérivées ...
Voici lénoncé :
Une fonction f définie sur R
f(x) = x(x+1)
x-2
1.étudiez son sens de variations de la fonction f ainsi que les limites aux bornes de son ensemble de définition (interprétez graphiquement ces résultats lorsquils le permettent)
JAI TROUVE pour la dérivé :
f(x) = x² - 4x -2
(x- 2)²
Mais après je bloque et cest quoi lensemble de définition de la dérivée ?
Merci pour votre aide ...
2) a. Montrez qu'il existe trois réels a, b, c tels que , pour tout x appartenant à R , on ait : f(x) = ax + b+ c/x-2
b. Soit delta la droite d'équation y = ax+b , pour les valeurs de a et b trouvées à la question a. Que représente la droite delta pour la courbe C ? ( justifiez)
c. Etudiez la position de C par rapport à la droite delta
d. déterminez le plus petit entier n tel que : si valeur absolu de x supérieur ou égal à n, alors valeur absolu de f(x) - ( ax+b) inférieur ou égal à 10^-1
e. trouvez tous les points de C dont les coordonnées sont des entiers relatif
suite après et oui c'est pas finit
bonjour!
voilà pour étudier les variations de ta fonction:
on sait que le signe de la dérivée dépend de (x²-4x-2) car (x-2)² >0
et, pour étudier le signe de (x²-4x-2) tu calcules son delta, soit:
b²-4ac
= 16- (-8)
= 24>0
soit X1= 2-(racine 6)
X2= 2+(racine 6)
ensuite tu peux faire un tableau de variation grace a l'étude du signe
sachant ke sur:
]-°°,2-(racine 6)[ et sur [2+(racine 6);+°°[ la dérivée est du signe contraire de a
et sur [2-(racine6): 2+(racine6)] la dérivée est du signe de a
sachant que la dérivée est définie sur R privée de 2
voila je crois ke c'est sa
voilà pour étudier les variations de ta fonction:
on sait que le signe de la dérivée dépend de (x²-4x-2) car (x-2)² >0
et, pour étudier le signe de (x²-4x-2) tu calcules son delta, soit:
b²-4ac
= 16- (-8)
= 24>0
soit X1= 2-(racine 6)
X2= 2+(racine 6)
ensuite tu peux faire un tableau de variation grace a l'étude du signe
sachant ke sur:
]-°°,2-(racine 6)[ et sur [2+(racine 6);+°°[ la dérivée est du signe contraire de a
et sur [2-(racine6): 2+(racine6)] la dérivée est du signe de a
sachant que la dérivée est définie sur R privée de 2
voila je crois ke c'est sa
|
Bonsoir à tous
C' est mon 1er message -réponse
On arouvé f'(x) =(x²-4x-2)/(x-2)²
dom f'= R\{2}
lLes Racines sont x'= 2-v6=-0,4 et x"= 2+v6= 4,4..
f(-0,4)=-0,23 et f(4,4)=6,2
Tableau des signes de f' et variations de f
x-oo.......-0,4......0.......1........2.........4,4......+oo
f'++++++++0------------------|-------0+++++++
f-oocr.....-1,2dec..0dec..0......|decr.....6,2 cr.....+oo
..............max..................................min
Bonsoir à tous
C' est mon 1er message -réponse
On arouvé f'(x) =(x²-4x-2)/(x-2)²
dom f'= R\{2}
lLes Racines sont x'= 2-v6=-0,4 et x"= 2+v6= 4,4..
f(-0,4)=-0,23 et f(4,4)=6,2
Tableau des signes de f' et variations de f
x-oo.......-0,4......0.......1........2.........4,4......+oo
f'++++++++0------------------|-------0+++++++
f-oocr.....-1,2dec..0dec..0......|decr.....6,2 cr.....+oo
..............max..................................min
oscar a écrit:
lLes Racines sont x'= 2-v6=-0,4 et x"= 2+v6= 4,4..
f(-0,4)=-0,23 et f(4,4)=6,2
Tableau des signes de f' et variations de f
x-oo.......-0,4......0.......1........2.........4,4......+oo
f'++++++++0------------------|-------0+++++++
f-oocr.....-1,2dec..0dec..0......|decr.....6,2 cr.....+oo
..............max..................................min
Bonjour Oscar , est - cece que tu as le droit d'arrondir dans un tableau de variation ?
Et je comprend pas tout à ton tableau , he is complicated ... :doh:
Salut,
on a=\frac{x(x-1)}{x-2}) avec Df=R-{2}
avec Df=R-{2}
il faut etudier les limites en -inf,+inf,2- et 2+
l'interpretation geometrique c'est d'eventuelle(s) asymptote(s)
donc tu as trouvé
c'est pas bon erreur de signe
}=\frac{x^2-4x+2}{(x-2)^2})
donc c'est du signe de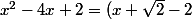(x-\sqrt{2}-2))
car (x-2)^2>0
donc essaie de faire ton tableau
on a
il faut etudier les limites en -inf,+inf,2- et 2+
l'interpretation geometrique c'est d'eventuelle(s) asymptote(s)
donc tu as trouvé
JAI TROUVE pour la dérivé :
f(x) = x² - 4x -2
(x- 2)²
c'est pas bon erreur de signe
donc c'est du signe de
car (x-2)^2>0
donc essaie de faire ton tableau
?
pour trouver le minimum je remplace par quoi ? c'est pas 2 le minimum ?!
et le maximum ? on remplace par 2-racine de 2 ?!
dur :doh:
et le maximum ? on remplace par 2-racine de 2 ?!
dur :doh:
! merci !
dac ! :we:
mais le truc c'est que j'obtient des valeurs approché , je peux quand même les mettre dans le tableau ?
mais le truc c'est que j'obtient des valeurs approché , je peux quand même les mettre dans le tableau ?
merci fonfon
merci c'est gentil !
j'ai mis la suite de l'exo , en fait j'avais oublie de la taper , jette y un coup d'oeil ! :we:
En tout cas merci encore pour ton aide ^^
j'ai mis la suite de l'exo , en fait j'avais oublie de la taper , jette y un coup d'oeil ! :we:
En tout cas merci encore pour ton aide ^^
2) a. Montrez qu'il existe trois réels a, b, c tels que , pour tout x appartenant à R , on ait : f(x) = ax + b+ c/x-2
b. Soit delta la droite d'équation y = ax+b , pour les valeurs de a et b trouvées à la question a. Que représente la droite delta pour la courbe C ? ( justifiez)
a) tu peux reduire au même denominateur ax+b+c/(x-2) et ensuite identifier les coefficients avec f(x)=(x²-x)/(x-2)
b) la droite delta sera asymptote oblique au voisinage de
alors si je réduit au même dénominateur sa me donne:
ax² - 2 ax +bx -2b + cx - 2c TOUT DIVISE PAR x -2
ensuite identifier les coefficients avec f(x)=(x²-x)/(x-2)
je ne comprend pas ?
ouin c'est ça mais il fut arranger un peu
or
rappel:2 polynôme sont egaux ssi ils ont le même degré avec les coefficients des temes de même degré egaux
donc on identifie
donc
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
