Bonjour. J'ai un problème avec un exercice sur les vecteurs.
Mon exercice est le suivant :
Dans le plan muni d'un repère, on donne les points :
A(2;4) B(2;-6) C(-4;-1)
a)Placer les opints A, B, et C.
( Ca c'est fait )
b) Calculer les coordonnées du point I vérifiant la relation 2IB(vecteur)+IC(vecteur)=0(vecteur)
c) Calculer les coordonnées du point K tel que :
3KA(vecteur)+2KB(vecteur)=0(vecteur)
Placer le point K.
d) On note (x;y) les coordonnées du point d'intersection G des droites (IA) et (KC).
En exprimant l'alignement des points G, I et A, puis des points G, K et C, calculer les coordronnées du point G.
Placer le point G.
e) Calculer les coordonnées du point L tel que:
AL(vecteur)=¼AC(vecteur)
Puis démontrer que les points B, G et L sont alignés.
Je suis bloquée à la question b).Je trouve I(0;13/3) et c'est faux.
Qqun pourait-il m'aider ?
Alignement et relations vectorielles
13 messages
- Page 1 sur 1
re
J'ai un problème.
Je comprends pas comment tu fais pour
"donc les coordonnées de G sont les solutions du systeme
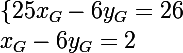
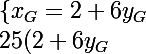-6y_G=26) "
"
comment tu passes de
25xG-6yG=26
à
25(2+6yG)-6yG=26
??
Je comprends pas comment tu fais pour
"donc les coordonnées de G sont les solutions du systeme
comment tu passes de
25xG-6yG=26
à
25(2+6yG)-6yG=26
??
Bonjour.
Pour la question e) j'ai calculé les coordonnées du point L.
Et puis montrer que les points B, G et L sont alignés j'ai montré que BG(vecteur) et BL(vecteur) sont colinéaires.
J'ai fait :
(xBL*yBG)-(xBG*yBL)=0
(-3/2 - 35/6) - (-1 * 35/4) = 0
-105/12 - (-35/4)=0
-150/12 + 35/4 = 0
35/4 = 105/12
8.75 = 8.75
Je ne suis pas sûre que ce soit la bonne rédaction pour prouver que les vecteur BG et BL sont colinéaires.
Qqun a la bonne rédaction ??
Pour la question e) j'ai calculé les coordonnées du point L.
Et puis montrer que les points B, G et L sont alignés j'ai montré que BG(vecteur) et BL(vecteur) sont colinéaires.
J'ai fait :
(xBL*yBG)-(xBG*yBL)=0
(-3/2 - 35/6) - (-1 * 35/4) = 0
-105/12 - (-35/4)=0
-150/12 + 35/4 = 0
35/4 = 105/12
8.75 = 8.75
Je ne suis pas sûre que ce soit la bonne rédaction pour prouver que les vecteur BG et BL sont colinéaires.
Qqun a la bonne rédaction ??
salut,
Bonjour.
jusqu'ici ça va:
apres il faut que tu montres que:
(y_L-y_G)-(y_G-y_B)(x_L-x_B)=0)
donc il faut que tu calcules:
(y_L-y_G)-(y_G-y_B)(x_L-x_B)) et que tu montres que ça vaut 0
et que tu montres que ça vaut 0
Bonjour.
Pour la question e) j'ai calculé les coordonnées du point L.
Et puis montrer que les points B, G et L sont alignés j'ai montré que BG(vecteur) et BL(vecteur) sont colinéaires.
jusqu'ici ça va:
apres il faut que tu montres que:
donc il faut que tu calcules:
ça c'est pas bon(xBL*yBG)-(xBG*yBL)=0
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
