Deux limites ...

par **Nisrina** » 12 Fév 2007, 11:55

bonjour ,

je bute sur ces deux limites , j'ai tenté toutes les méthodes et les astuces que je connais mais je tombe toujours sur une FI :mur:

1)

2)

voilà si vous avez des pistes à me proposer ça sera très gentil :we:

bonne journée !

EDIT: shuut!! il parait que c'est pas le bon endroit à poster mon mess. , comment fait-on pour déplacer un sujet ?

par **darkmarth** » 12 Fév 2007, 11:56

as tu essayé de résoudre séparement par un changement de variable ?

par **Nisrina** » 12 Fév 2007, 11:59

oui j'ai essayé , mais j'obtiens toujours une FI.

par **mathelot** » 12 Fév 2007, 12:31

pour la (1), poser

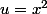
quand

puis

pour la (2), c'est bourrin, suffit de faire les calculs.
rappelle toi les DL de sin(x),

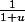
et

par **Nisrina** » 12 Fév 2007, 12:48

bonjour,

j'ai essayé ce cvd pour la 1ère , mais je tombe tj sur une FI

pour le 2ème j'ai pas vu le DL , je suis en TS .

par **mathelot** » 12 Fév 2007, 13:10

pour la (1):
on pose, quand

,

sinon, que connais tu ? les petits "o" ? , les "

",
les différentielles ?

par **Nisrina** » 12 Fév 2007, 13:28

il me semble que :

nan ?

sinon, que connais tu ? les petits "o" ? , les "",
les différentielles ?

non je ne connais pas , dsl .

par **mathelot** » 12 Fév 2007, 13:36

Que connais tu ?

par **Nisrina** » 12 Fév 2007, 13:40

les outils modestes de terminal , les limites remarquables de ln , dérivation , changement de variable .

par **mathelot** » 12 Fév 2007, 15:04

la question (1) est difficile avec des outils de terminale:
une chose est sûre, on peut utiliser les équivalents dans les produits et les quotients mais pas dans les sommes. j'ai un peu avançé:

puis que:

peut être peux tu conclure avec ça ?

par **Nisrina** » 12 Fév 2007, 15:17

merci bien pour ton aide , mais je ne peux pas non plus utiliser ces équivalents , c'est pas encore vus :triste:

par **amine801** » 12 Fév 2007, 15:38

slt
as tu une limite usuel dans ton cour du genre?

par **Nisrina** » 12 Fév 2007, 15:42

oui je l'ai .

par **amine801** » 12 Fév 2007, 15:47

alors tu peut poser

vu que

tu peut multiplier et divise par (u-1)
pour utilise la limite si dessus

par **mathelot** » 12 Fév 2007, 15:57

mathelot a écrit:

cet équivalent là est au programme et il fait avancer le schmilblick.
c'est

si tu l'avais pas reconnu.
et le 2ème c'est

(j'ai réduit au même dénominateur)

fahr, peux tu nous aider ? uniquement avec des thm de terminale ?

par **amine801** » 12 Fév 2007, 16:10

Ecoute mathelot si nisrina dit quelle a pas vu déquivalence moi jessaye
De faire sans Il faut pas te sentir vise
Et puis jai pas fait le bac français nous on voie cest truc en première ou second
Donc permet davoir des doutes sur le contenue des programmes
Rassure-toi léquivalence je connais bien
En plus je voit pas en quoi ce que jai dit ne fait pas avancer le schm.
:zen:

par **mathelot** » 12 Fév 2007, 16:14

oui, tu as raison. Il faut sans doute remplacer

par

perso, je laisse tomber, j'étais en Terminale en 1970...
PS: je te rassure, le schmilblick n'est pas du tout un gros mot, ça fait référence à une blague hilarante.

par **amine801** » 12 Fév 2007, 16:22

mathelot a écrit:PS: je te rassure, le schmilblick n'est pas du tout un gros mot, ça fait référence à une blague hilarante.

:++:
Je sais bien mais cest un mot qui a suscité souvent une difficulté de prononciation doù les petits:we::we::we:

par **Nisrina** » 12 Fév 2007, 19:36

mathelot a écrit:cet équivalent là est au programme et il fait avancer le schmilblick.
c'est si tu l'avais pas reconnu.
et le 2ème c'est (j'ai réduit au même dénominateur)

oui mathelot je comprends trés bien cela , et ces équivalents me paraissent tt à fait logiques , mais quoi dire du programme ! j'ai pas le droit de les utiliser , c'est vrai que c'est simple mais si la question était posée ainsi c'est qu'il y a sans doute une issue (sûrement plus compliquée :hum:) .

amine--- j'arrive pas à lever l'indetermination pour

merci :we:

par **amine801** » 12 Fév 2007, 19:51

mais au meme denominateur apres il faut multiplier et diviser par

apres avoir utilise l'identite remarquable factorise par x^2

Deux limites ...

deux limites ...

Qui est en ligne